Question

Water from a tap emerges vertically downwards with initial velocity ${{4 m/s}}$. The cross-sectional area of the tap is ${{A}}$. The flow is steady and pressure is constant through the water. The distance ${{h}}$vertically below the tap, where the cross-sectional area will becomes $\left( {\dfrac{{{2}}}{{{3}}}} \right){{A}}$ is: $\left( {{{g = 10 cm/}}{{{s}}^{{2}}}} \right)$.

Answer 1

Hint: First of all, write the equation of continuity i.e. and then substitute the given value in that equation. Then use Bernoulli’s theorem given as:${{\rho + \rho g}}{{{h}}_{{1}}}{{ + }}\dfrac{{{1}}}{{{2}}}{{\rho }}{{{v}}_{{1}}}^{{2}}{{ = \rho + \rho g}}{{{h}}_2}{{ + }}\dfrac{{{1}}}{{{2}}}{{\rho }}{{{v}}_2}^{{2}}$and then substitute the values in the formula and solve.

Complete step by step solution:
Equation of continuity

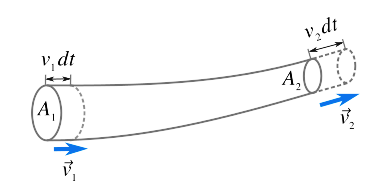
Let us consider a non-viscous, incompressible liquid which is flowing steadily through a pipe. Let ${{{A}}_{{1}}}$ be the cross-section, ${{{v}}_{{1}}}$ be the fluid velocity, ${{{\rho }}_{{1}}}$ be the fluid density at point ${{A}}$(left end of the pipe). And Let ${{{A}}_2}$ be the cross-section, ${{{v}}_2}$ be the fluid velocity, ${{{\rho }}_2}$ be the fluid density at point ${{B}}$(right end of the pipe).
The area of cross-sections are made such that.
Now, formula for mass is given by
And volume can be rewritten as ${{{A}}_{{1}}}{{ > }}{{{A}}_{{2}}}$ the product of area of cross section and length.
Thus, ${{m = \text{area of cross section} }} \times {{ length \times density}}$
Therefore, mass of fluid flowing through section A in small time dt is given by
${{{m}}_{{1}}}{{ = }}{{{a}}_{{1}}}{{ }}{{{v}}_{{1}}}{{ dt }}{{{\rho }}_{{1}}}$
Similarly, mass of fluid flowing through section B in small time dt is given by
${{{m}}_2}{{ = }}{{{a}}_2}{{ }}{{{v}}_2}{{ dt }}{{{\rho }}_2}$
By conservation of mass,
${{{m}}_{{1}}}{{ = }}{{{m}}_{{2}}}$
${{ }}{{{a}}_{{1}}}{{ }}{{{v}}_{{1}}}{{ dt }}{{{\rho }}_{{1}}} = {{ }}{{{a}}_2}{{ }}{{{v}}_2}{{ dt }}{{{\rho }}_2}$
As the fluid is incompressible, so ${{{\rho }}_{{1}}}{{ = }}{{{\rho }}_{{2}}}$
Hence ${{ }}{{{a}}_{{1}}}{{ }}{{{v}}_{{1}}} = {{ }}{{{a}}_2}{{ }}{{{v}}_2}$
On substituting values in above formula, we get
\[ {{ A \times 4 = }}\dfrac{{{2}}}{{{3}}}{{ A}}{{{v}}_{{2}}} \\
   \Rightarrow {{ }}{{{v}}_{{1}}}{{ = 6 m/s}} \\
 \]
Now using Bernoulli’s theorem
${{\rho + \rho g}}{{{h}}_{{1}}}{{ + }}\dfrac{{{1}}}{{{2}}}{{\rho }}{{{v}}_{{1}}}^{{2}}{{ = \rho + \rho g}}{{{h}}_2}{{ + }}\dfrac{{{1}}}{{{2}}}{{\rho }}{{{v}}_2}^{{2}}$
On further simplification, we get
$
  {{g(}}{{{h}}_{{1}}}{{ - }}{{{h}}_{{2}}}{{) = }}\dfrac{{{1}}}{{{2}}}{{(}}{{{v}}_{{2}}}^{{2}}{{ - }}{{{v}}_{{1}}}^{{2}}{{)}} \\
   \Rightarrow {{g(h) = }}\dfrac{{{1}}}{{{2}}}{{(}}{{{v}}_{{2}}}^{{2}}{{ - }}{{{v}}_{{1}}}^{{2}}{{)}} \\
$
On substituting values, we get
$
  {{g(h) = }}\dfrac{{{1}}}{{{2}}}{{(}}{{{6}}^{{2}}}{{ - }}{{{4}}^{{2}}}{{)}} \\
   \Rightarrow {{10 \times h = }}\dfrac{{{1}}}{{{2}}}{{(36 - 16)}} \\
  \therefore {{h = 1 m}} \\
$
Thus, the value of h is ${{1 m}}$.

Note: Equation of continuity states that during streamlines flow of the non-viscous and incompressible fluid through pipes of varying cross-section, the product of area of cross-section and the normal fluid velocity remains constant throughout the flow.