Question

How is the volume versus temperature graph for a sample of an ideal gas at constant pressure?

Answer 1

Hint: To answer this question, we should know about the relationship between volume and temperature. This relationship was given by Charles’ law. By using this law we can easily find out the answer.

Complete step by step answer:
> To answer this question, we should know about Charles’ law. We should know that Charles’ law is one of the gas laws which explain the relationship between volume and temperature of a gas. Charles’s law states that when pressure is held constant, the volume of a fixed amount of dry gas is directly proportional to its absolute temperature. It should be noted that, when we take two measurements in direct proportion then any change made in one of them affects the other through direct variation. Charles’ Law is expressed by the equation:
\[\begin{align}
  & V\alpha T \\
 & \dfrac{V1}{T1}=\dfrac{V2}{T2} \\
\end{align}\]
> From the above expression we should know that V1 and V2 are the Initial Volumes and Final Volume respectively. T1 refers to the Initial Temperature and T2 refers to the Final Temperature.
> We can understand this by taking one example, we should know that on heating up a fixed mass of gas, that is, increasing the temperature, the volume also increases. Similarly, on cooling, the volume of the gas decreases.
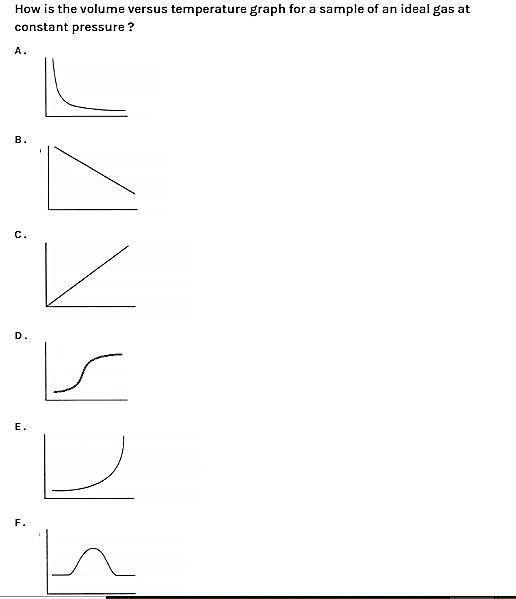
So, from this we can now say that option C is correct. In this graph we can say that it is a straight line because volume and temperature are directly proportional.

Note: It is important to discuss that the unit Kelvin is preferred for solving problems related to Charles Law, and not Celsius. Kelvin (T) is also known as the Absolute temperature scale. We should know about Charles' law application in real life. It has a wide range of applications. Helium balloons shrink in a cold environment. Second example is this : while jogging in winters, we face difficulty because our lung capacity decreases.