Question

Underwater illusion. One clue used by your brain to determine the direction of a source of sound is the time delay Δt between the arrival of the sound at the ear closer to the source and the arrival at the farther ear. Assume that the source is distant so that a wavefront from it is approximately planar when it reaches you, and let D represent the separation between your ears.
(a) If the source is located at angle θ in front of you (Fig. 17-31), what is Δt in terms of D and the speed of sound v in air?
(b) If you are submerged in water and the sound source is directly to your right, what is Δt in terms of D and the speed of sound \[{{v}_{w}}\] in water?
(c) Based on the time-delay clue, your brain interprets the submerged sound to arrive at an angle θ from the forward direction. Evaluate θ for fresh water at 20 \[^{0}C\]

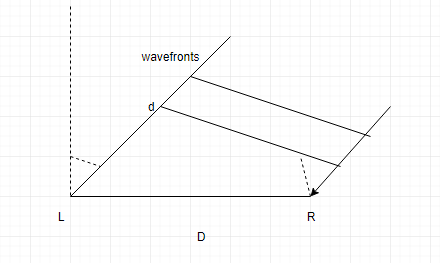
The two angles marked in the figure represent angle, θ

Answer 1

Hint: Wavefront describes the movement of sound from the source and has its origin in Hygen’s principle. According to it, Sound moves equally in all directions and there cannot be a backward flow of energy and hence no backward wavefront. We can make use of formula for speed to find out the answer of part (a)

Complete Step by step solution:
(a) using the relationship between speed, distance and time we get.
\[\Delta t=\dfrac{d}{v}=\dfrac{D\sin \theta }{v}\]
(b) since, the speed of the sound in water is now \[{{v}_{n}}\] with \[\theta ={{90}^{0}}\], we have
\[\Delta {{t}_{w}}=\dfrac{D\sin \theta }{{{v}_{w}}}=\dfrac{d}{{{v}_{w}}}\]
(c) now to find the apparent angle we can do that as, \[\Delta t=\dfrac{D\sin \theta }{v}=\dfrac{d}{{{v}_{w}}}\]
Solving for the angle \[\theta \]with \[{{v}_{w}}=1482m/s\] we get,
$\Rightarrow \theta ={{\sin }^{-1}}(\dfrac{v}{{{v}_{w}}}) \\
\Rightarrow \theta ={{\sin }^{-1}}(\dfrac{343}{1482}) \\$
$343m/s$ being the speed of sound in air,
$\Rightarrow {{\sin }^{-1}}(0.231) \\
\therefore {{13}^{0}} \\$

Note: Trigonometric ratios are unitless but angles can be measured either in degrees or radians. All the units to be taken in standard SI units of system. A wavefront is a surface over which a wave has a constant phase. Wavefront came into existence from Hygen’s theory of wave picture of light. Wavefront determines the nature and propagation of a light emanating from the given source.
One should always keep in mind that frequency is the characteristic of the source of the light