Question

Two wheels are constructed, as shown in Figure with four spokes. The wheels are mounted one behind the other so that an observer normally sees a total of eight spokes but only four spokes are seen when they happen to align with one another. If one wheel spins at $6\, rev{\min ^{ - 1}}$ , while other spins at $8\,rev {\min ^{ - 1}}$ in same sense, how often does the observer see only four spokes?

A) $4$ times a minute
B) $6$ times a minute
C) $8$ times a minute
D) Once in a minute

Answer 1

Hint: This problem is not based on the formula calculation, it is completely based on the analysis of the given question and solving. Due to the rotation of the wheel, the angular displacement should be taken as $\pi $ and the angular velocity should be taken as $\omega $.

Complete step by step solution:
It is given that the
Angular velocity of one wheel, $\omega = 6\,rev{\min ^{ - 1}}$
Angular velocity of other wheel, $\omega = 8\,rev{\min ^{ - 1}}$
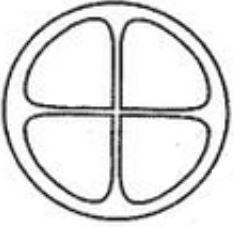
Let us understand the condition in the question, that the observed can see the four spokes only when the difference in the angular displacement is:
$\Rightarrow$ $n\dfrac{{2\pi }}{4} = n\dfrac{\pi }{2}$
Hence the $n$ represents the number of times the observer can see only four spokes and the $\dfrac{\pi }{2}$ is the angular displacement of the first wheel in relation to each other. Let us consider that the observer can see the wheel spokes in a one minute period of time.
$\Rightarrow$ $2 \times 2\pi = 4\pi $
The above step can also be simplified as
$\Rightarrow$ $8\dfrac{\pi }{2}$
Hence the observer can see only four spokes $8$ times.

Thus the option (C) is correct.

Note: Remember that the spokes are the rods that join the centre of the wheel to its periphery in order to provide the structural support to the wheel and also stability to it. The calculated number of times holds only for a minute of a time.