Question

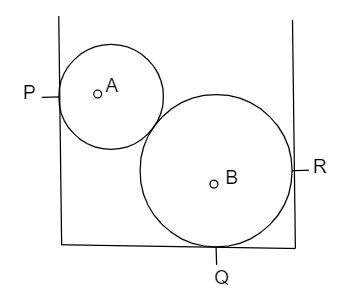
Two steel balls $A$ and $B$ are placed inside a right circular cylinder of diameter $54\,cm$ making contacts at points $P$ , $Q$ and $R$ as shown. The radius ${r_A} = 12\,cm$ and ${r_B} = 18\,cm$ . The masses are ${m_A} = 15\,Kg$ and ${m_B} = 60\,Kg$ . The forces exerted by the floor at a point $Q$ and the wall at $R$ are respectively (taking $g = 10\,m{s^{ - 2}}$ ).

Answer 1

Hint: Use the given force formula below , and calculate the normal force that acts along the line $AB$ formed by the spherical $A$ and the spherical ball $B$ . From the obtained force value calculate the force acts on the point $Q$ due to the floor.

Formula used:
The formula of the force is given by
$F = mg\cos \theta $
Where $F$ is the force exerted, $m$ is the mass of the object, $g$ is the acceleration due to gravity and $\theta $ is the angle made by the force.

Complete step by step solution:
It is given that the
Diameter of the right circular cylinder, $d = 54\,cm$
The radius of the first steel ball, ${r_1} = 12\,cm$
The radius of the second steel ball, ${r_2} = 18\,cm$
The mass of the first steel ball, ${m_1} = 15\,Kg$
The mass of the second steel ball, ${m_2} = 60\,Kg$
The acceleration due to gravity, $g = 10\,m{s^{ - 2}}$

The force exerted at a point $Q$ will be due to both the spherical ball $A$ and the ball $B$ .
Using the formula of the force,
$\Rightarrow {N_{AB}} = {m_1}g\cos \theta $
Substituting the known parameters in the above formula,
$\Rightarrow {N_{AB}} = 15 \times 10 \times \cos {45^ \circ }$
By multiplying the parameters in the above equation,
$\Rightarrow {N_{AB}} = \dfrac{{150}}{{\sqrt 2 }}\,N$
At the point $Q$ , The force formed due to the line $AB$ acts at the angle ${45^ \circ }$ with the perpendicular.
$\Rightarrow {N_Q} = {N_{AB}}\cos {45^ \circ }$
By substituting the value of the force normal to $AB$ in the above equation,
$\Rightarrow {N_Q} = \dfrac{{150}}{{\sqrt 2 }}\cos {45^ \circ }$
By further simplification of the above equation,
$\Rightarrow {N_Q} = 75\,N$

Hence the floor exerted by the floor at $Q$ is $75\,N$.

Note: The angle ${45^ \circ }$ is formed by the joining of the centre of the spherical ball $A$ and $B$ with that of the horizontal. The weight of the ball along with the acceleration due to gravity of $A$ acts perpendicular downwards constituting the normal line $AB$ .