Question

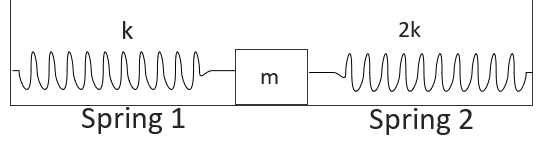
Two springs of force constant k and 2k are connected to a mass shown in figure. The frequency of oscillation of the mass is:

Answer 1

Hint: For the given mass try deriving the equilibrium position of the mass and due to the disturbance. Find the forces generated due to each spring using the equation ${{F}_{\text{spring restoring}}}=-kx$ and equate the total force on the block of mass. Therefore, get the resultant spring constant for the setup, find the frequency of oscillation from the formula.

Complete step-by-step answer:
Block is displaced by a distance x from its equilibrium position, it gets stretched or compressed. Spring will try to get its earlier position back and exert a force (spring restoring) on the block, which is given by;
${{F}_{\text{spring restoring}}}=-kx$
Where,
k is the spring constant
x is the displacement of the block from its equilibrium position.
Negative sign shows that spring is trying to pull back the block in the opposite direction to its motion.
When spring is stretched, potential energy is stored in the spring. This potential energy gets converted into kinetic energy for the block and block move toward its equilibrium position. When the block comes to its equilibrium position, it will have some kinetic energy and will move in the opposite direction, and it will compress spring. Thus, the block starts oscillating with respect to its equilibrium position.
Frequency of this oscillation is given by
$\omega =\sqrt{\dfrac{k}{m}}$
Where,
k is the spring constant
m is the mass of the block.
Here block is attached to two springs as shown in the above diagram. So, when we displace the block to x distance, one spring will get compressed and another will get stretched. Both springs will try to get their prior state and push the block to its equilibrium position. Thus, both the spring forces will act on block in the same direction for every possible disturbance.
Assume, if mass is pushed left, spring 1 will push the block towards right. Similarly, the spring 2 will pull the block towards right.
In the above given question both the springs are working and exerting force on the block in the same direction, so net spring force exerted on the block can be given by;
${{F}_{\text{spring restoring}}}=-kx-2kx$
Where,
k, and 2k are the spring constants of both the springs
${{F}_{\text{spring restoring}}}=-3kx$
So, net effective spring constant will be 3k.
Now we can find out frequency;
$\omega =\sqrt{\dfrac{{{k}_{eff}}}{m}}$
After putting the value of ${{k}_{eff}}$, we get our answer
$\omega =\sqrt{\dfrac{3k}{m}}$
Now we know, $\omega =2\pi f$, so above equation can be written as,
$\begin{align}
  & 2\pi f=\sqrt{\dfrac{3k}{m}} \\
 & \Rightarrow f=\dfrac{1}{2\pi }\sqrt{\dfrac{3k}{m}} \\
\end{align}$
Hence, the frequency of oscillation of the mass is $f=\dfrac{1}{2\pi }\sqrt{\dfrac{3k}{m}}$.

Note: For an oscillation motion of block, initial displacement of block must be small. Spring restoring force is only valid for small values of x. Spring constant can be given by
$k=\dfrac{YA}{L}$
Where Y is the young’s modulus, A is the area over which force is acting, L is the length of spring.
Young’s modulus is further defined as
$\begin{align}
  & Y=\dfrac{\text{Stress}}{\text{Strain}} \\
 & \Rightarrow Y=\dfrac{\dfrac{F}{A}}{\dfrac{{{D}_{L}}}{L}} \\
\end{align}$
Where${{D}_{L}}$ is the extension in the wire of length L.