Question

Two satellites A and B of masses 200 kg and 400 kg are revolving round the earth at height of 600 km and 1600 km respectively.
If $T_A$ and $T_B$ are the time periods of A and B respectively then the value of ${T_B} – {T_A}$:

[Given: Radius of earth = 6400 km, mass of earth = $6\times {10^24} kg$]
(A) $4.24 \times {10^2} s$
(B) $3.33\times {10^2} s$
(C) $1.33 \times {10^3} s$
(D) $4.24 \times {10^3} s$

Answer 1

Hint: Since no specific details of the trajectory is given, we will take the circular orbit as the path of the satellite. Now we can find the velocity of the satellite by equating the gravitational force equal to the centripetal force. From this we can calculate the time period of revolution as the speed and the distance covered in one revolution is given to us.

Formula used:
${F_G} = \dfrac{{GMm}}{{{r^2}}}$
${F_C} = \dfrac{{m{v^2}}}{r}$

Complete answer:
From the diagram given below we can find the velocity of the object 'S' by using the above given formula.

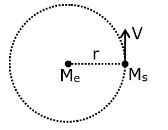
${F_G} = \dfrac{{G{M_e}{M_S}}}{{{r^2}}}$is the force of gravitation.
${F_C} = \dfrac{{{M_S}{v^2}}}{r}$ is the centripetal force.

Since both of them are equal we can equate them to find the value of velocity.
$\dfrac{{{M_S}{v^2}}}{r} = \dfrac{{G{M_e}{M_S}}}{{{r^2}}}$
$ \Rightarrow v = \sqrt {\dfrac{{G{M_e}}}{r}} $
This shows that velocity does not depend on the mass of the object.

We have the velocity of the object, we can find the velocity of the masses by replacing each of the variables with the respective values for the masses A and B.

Since it is a circular orbit the total distance is $2\pi r$ where r is the distance from the centre of the earth to the masses. The time period of revolution is:
$T = \dfrac{{2\pi r}}{v} = \dfrac{{2\pi r}}{{\sqrt {\dfrac{{G{M_e}}}{r}} }}$ where $v = \sqrt {\dfrac{{G{M_e}}}{r}} $
$ \Rightarrow T = \sqrt {\dfrac{{4{\pi ^2}{r^3}}}{{G{M_e}}}} $

The time period is proportional with the distance from the centre, we only need to worry about the distance only. Thus, the difference of their time period will be
\[{T_B} - {T_A} = \sqrt {\dfrac{{4{\pi ^2}{r_B}^3}}{{G{M_e}}}} - \sqrt {\dfrac{{4{\pi ^2}{r_A}^3}}{{G{M_e}}}} \]
\[{T_B} - {T_A} = \dfrac{{2\pi }}{{\sqrt {G{M_e}} }}\left( {{r_B}^{\dfrac{3}{2}} - {r_A}^{\dfrac{3}{2}}} \right)\]
\[{T_B} - {T_A} = \dfrac{{2\pi }}{{\sqrt {G{M_e}} }}\left( {{{\left( {1600} \right)}^{\dfrac{3}{2}}} - {{\left( {600} \right)}^{\dfrac{3}{2}}}} \right)\]
\[{T_B} - {T_A} = 1.33 \times {10^3}s\]

Thus, the difference in their time period will be $1.33 \times {10^3} s$. The correct option is (C).

Note: Rather than deriving the formula of the velocity it is quite useful to note that the formula for a masses revolving around earth is equal to where M is the mass of the earth G is the gravitational constant and r is the distance from the centre of the earth is $v = \sqrt {\dfrac{{G{M_e}}}{r}} $
We can also use the Kepler's law to find the proportional factor of time period as we know that$\left( {{T^2} \propto {R^3}} \right)$ where T is the time period and R is the distance from the centre of the earth or a mass object.