Question

Two points of a rod move with velocities 3 v & v perpendicular to the rod and in the same direction, separated by a distance 'r'. The angular velocity of rod is:
A. $\omega = \dfrac{{3v}}{r}$
B. $\omega = \dfrac{{4v}}{r}$
C. $\omega = \dfrac{{5v}}{r}$
D. $\omega = \dfrac{{2v}}{r}$

Answer 1

Hint: We must apply the angular velocity formula in order to answer this question. Let's first discuss angular velocity, the vector measure of rotation rate, which describes the rate at which an item rotates or revolves in relation to another point.

Formula used:
$v = r\omega $

Complete answer:
A rotating object's point continually changes direction, making it challenging to determine the angular velocity direction. The rotating object's axis is the only location where its direction is fixed. The Right Hand Rule is used to identify the direction of angular velocity using the axis of rotation.

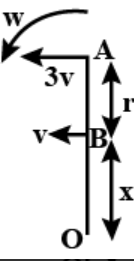
In the given diagram we can see that the upper point of the rod A is moving with velocity 3v which is perpendicular to the rod. Also, at point B the velocity is given v perpendicular to rod. Let us assume the distance between point A and the point B is r and the distance between point B and point O is x. Hence, the total length of rod will be r+x,

Let us assume the angular velocity of rod about the point O is$\omega $. Formula we will use will be
$v = r\omega $

For point A we can write the equation as,
$3v = \left(r + x\right)\omega $-----(1)

Also, for point B we can write as
$v = x\omega $--------(2)

Now, subtracting equation 2 from 1 we get,
$2v = r\omega $
$ \Rightarrow \omega = \dfrac{{2v}}{r}$

Hence, option D is correct.

Note: The obtained linear velocity turns out to be proportional to the radius of the rotating particle's circle. Every single particle in a revolving body has the same angular velocity. We may deduce the relationship between any other linear and rotational variable from this relationship. For instance, the radius times the angular acceleration is also equal to the linear acceleration.