Question

Two identical cylindrical vessels, with their bases at the same level, each contain a liquid of density $\rho $. The height in one vessel is ${h_1}$ and that in the other is ${h_2}$. The area of either base is A. What is the work done by gravity in equalising the levels when the vessels are interconnected:
A) $A\rho g{\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}$.
B) $A\rho g{\left( {\dfrac{{{h_1} + {h_2}}}{2}} \right)^2}$.
C) $\dfrac{1}{2}A\rho g{\left( {{h_1} - {h_2}} \right)^2}$.
D) $\text{None of these.}$

Answer 1

Hint: The work done is defined as the energy required as to move an object for some distance. The product of applied force and distance is known as work done and it is represented in terms of joules. Density is defined as the ratio of mass and volume.

Formula used: The formula of work done is given by,
$ \Rightarrow W = mgh$
Where mass is m, the height is h and the acceleration due to gravity is g.

Complete step by step solution:
It is given in the problem that two identical cylindrical vessels, with their bases at the same level, each contain a liquid of density $\rho $ the height in one vessel in ${h_1}$ and that in the other is ${h_2}$ the area of either base is A we need to find the work done by gravity in equalising the levels when the vessels are interconnected and we need to select the correct answer for this problem.

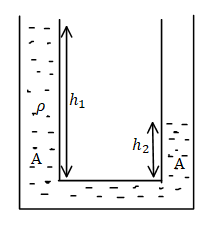
Let the height h be equal to,
$ \Rightarrow h = \dfrac{{{h_1} + {h_2}}}{2}$
The decrease in height in the vessel of height${h_1}$.
$ \Rightarrow \Delta h = {h_1} - \left( {\dfrac{{{h_1} + {h_2}}}{2}} \right)$
$ \Rightarrow \Delta h = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)$
Mass of the liquid is equal to,
$ \Rightarrow m = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)\rho A$
The formula of work done is given by,
$ \Rightarrow W = mgh$
Where mass is m, the height is h and the acceleration due to gravity is g.
$ \Rightarrow W = mgh$
$ \Rightarrow W = \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right) \times \rho A \times g \times \left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)$
$ \Rightarrow W = {\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}A\rho g$
The work done is equal to $W = {\left( {\dfrac{{{h_1} - {h_2}}}{2}} \right)^2}A\rho g$.

The correct answer for this problem is option A.

Note: The students are advised to understand and remember the formula of the work done as it is very useful in solving these kinds of problems. Whenever two columns are attached and they are having the same liquid with different levels then they come to the same level as the liquid flows from high pressure to low pressure and it stops when the liquid levels.