Question

Two communicating vessels contain mercury. The diameter of one vessel is n times larger than the diameter of the other. A column of water of height h is poured into the left vessel. The mercury level will rise in the right hand vessel (s=relative density of mercury and ρ =density of water) by:

$\eqalign{
  & {\text{A) }}\dfrac{{{{\text{n}}^{\text{2}}}{\text{h}}}}{{{{{\text{(n + 1)}}}^{\text{2}}}{\text{s}}}} \cr
  & {\text{B)}}\dfrac{{\text{h}}}{{{\text{(}}{{\text{n}}^{\text{2}}}{\text{ + 1)s}}}} \cr
  & {\text{C)}}\dfrac{{\text{h}}}{{{{{\text{(n + 1)}}}^{\text{2}}}{\text{s}}}} \cr
  & {\text{D)}}\dfrac{{\text{h}}}{{{{\text{n}}^{\text{2}}}{\text{s}}}} \cr} $

Answer 1

Hint: We will follow Pascal's principle, also called Pascal's law, any force applied to a confined fluid is transmitted uniformly in all directions throughout the fluid regardless of the shape of the container.

Complete step by step solution:
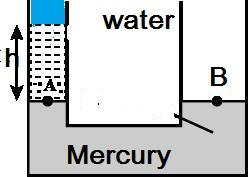
If the level in narrow tubes goes down by $h_1$, then in broader tube goes up to $h_2$
$\eqalign{
  & \Rightarrow \pi {r^2}h_1 = \pi {(nr)^2}h_2 \cr
  & \Rightarrow h_1 = {n^2}h_2 \cr
  & {\text{Now pressure at point A = pressure at point B}} \cr
  & {\text{h}}\rho {{g = (h_1 + h_2)}}\rho {\text{'g}} \cr
  & \Rightarrow {\text{h = (}}{{\text{n}}^2}h_2 + h_2)sg \cr
  & {\text{also s = }}\dfrac{{\rho {\text{'}}}}{\rho } \cr
  & h_2 = \dfrac{h}{{({n^2} + 1)s}} \cr} $

Option B is correct.

Additional Information: A solid surface can exert pressure, but liquids (ie liquid or gas) can also exert pressure. It may sound strange if you think about it because it is hard to imagine hitting a hammer in a nail with liquid. To understand this, imagine sinking to some depth in water. Due to the force of gravity, the water above you will be pulled down and this will increase the pressure on you. If you go deeper, you will have more water, so the weight and pressure will also increase with the water.
The pressure in a fluid depends on the height of the fluid column, but not on the shape of the vessel in which it is contained, when we assume that wherever the fluid is in contact with the vessel wall, the force between it and the wall Perpendicular to the surface.

Note: Pressure exerted by liquid changes with the depth in liquid. Value of pressure is small just below the surface of the liquid, but as we go deeper, the pressure increases with the depth. All liquids have weight and exerts pressure at the bottom of the container. In SI units, the unit of pressure is Pascal (Pa), which is equal to $N / {m^2}$.The primary mathematical expression for pressure is given by: ${\text{pressure = }}\dfrac{{force}}{{area}}$.