Question

Two boys are standing at the ends A and B of a ground, where \[AB = a\]. The boy at B starts running in a direction perpendicular to AB with velocity \[{v_1}\]​. The boy at A starts running simultaneously with velocity $v$ and catches the other boy in a time t, where t is:
A) \[\dfrac{a}{{\sqrt {{v^2} + v_1^2} }}\]
B) \[\sqrt {\dfrac{{{a^2}}}{{{v^2} - v_1^2}}} \]
C) \[\dfrac{a}{{v + {v_1}}}\]
D) \[\dfrac{a}{{v - {v_1}}}\]

Answer 1

Hint: First we see that according to the question, at which direction the boy B is moving. Then draw a figure to calculate time t at which Boy at A catches boy which runs from B. We use Pythagoras’s theorem to calculate time. According to the question, both boys are running along the sides of the right angle triangle.

Complete step by step solution:
First we draw diagram indicating directions of velocities of boys moving from A and B

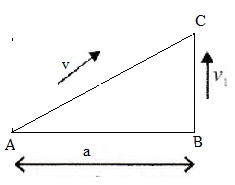
Given: Width of ground, \[AB = a\], velocity of boy moving from point B=\[{v_1}\], velocity of boy moving from point A=\[v\]
From figure, directions of\[{v_1}\], \[v\] and AB are making sides of right angle triangle
Use Pythagoras theorem, \[A{C^2} = A{B^2} + B{C^2}\]......(I)
Distance AC is given by, \[AC = velocity{\text{ }}of{\text{ }}boy{\text{ }}moving{\text{ }}from{\text{ }}B{\text{ }} \times time{\text{ }}taken{\text{ }}from{\text{ }}A{\text{ }}to{\text{ }}C\]
\[ \Rightarrow AC = vt\]
Distance AB is given by \[AB = a\]
Distance BC is given by, \[BC = {v_1}t\]
Substituting values of AB,BC and CA in equation (i), we get
\[{\left( {vt} \right)^2} = {\left( a \right)^2} + {\left( {{v_1}t} \right)^2}\]
\[\begin{gathered}
   \Rightarrow {v^2}{t^2} = {a^2} + v_1^2{t^2} \\
  {v^2}{t^2} - v_1^2{t^2} = {a^2} \\
   \Rightarrow \left( {{v^2} - v_1^2} \right){t^2} = {a^2} \\
  \therefore {t^2} = \dfrac{{{a^2}}}{{\left( {{v^2} - v_1^2} \right)}} \\
\end{gathered} \]
\[ \Rightarrow t = \sqrt {\dfrac{{{a^2}}}{{\left( {{v^2} - v_1^2} \right)}}} \]
Time required for boy running from A to catches the other boy running from B is given by,
$\Rightarrow$ \[t = \sqrt {\dfrac{{{a^2}}}{{\left( {{v^2} - v_1^2} \right)}}} \]

Hence, the correct option is D.

Additional information: Pythagoras theorem describes the relation between the lengths of the sides a, b and c of the right angle triangle. This relation is called the "Pythagorean equation": This theorem is also called the Pythagorean Theorem. According to Pythagoras theorem “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle are called Perpendicular, Base and Hypotenuse.

Note: Students must be careful about making figures according to directions of velocities. Because the correct figure calculates the write value of time. By Pythagoras theorem, only distance is calculated. Distance is calculated by velocity and time. Students must be careful to apply Pythagoras theorem and distance value.