Question

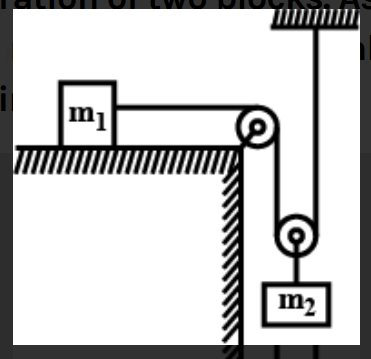
Two blocks of masses $m_{1}=1.5 k g$ and $m_{2}=2 k g$ are attached to each other by strings and pulleys as shown in figure. Assume that pulleys are massless and frictionless and strings are massless. The system is released. If the table is frictionless, find the acceleration of $m_{1}$ and $m_{2. }$ Take $g=10 m s^{-2}$

A) $5 m s^{-2}$ and $2.5 m s^{-2}$
B) $10 m s^{-2}$ and $5 m s^{-2}$
C) $15 m s^{-2}$ and $7.5 m s^{-2}$
D) $20 m s^{-2}$ and $10 m s^{-2}$

Answer 1

Hint: We know that tension is nothing but the drawing force acting on the body when it is hung from objects like chain, cable, string etc. It is represented by T. The direction of tension is the pull which is given the name tension. Thus, the tension will point away from the mass in the direction of the string or rope. In case of the hanging mass, the string pulls it upwards, so the string or rope exerts an upper force on the mass and the tension will be on the upper side. The tension force is the force that is transmitted through a string, rope, cable or wire when it is pulled tight by forces acting from opposite ends. The tension force is directed along the length of the wire and pulls equally on the objects on the opposite ends of the wire. Based on this concept we have to solve this question.

Complete step by step answer
We should know that velocity is defined as the rate change of displacement per unit time. Speed in a specific direction is also known as velocity. Velocity is equal to displacement divided by time. Speed, being a scalar quantity, is the rate at which an object covers distance. The average speed is the distance which is a scalar quantity per time ratio. On the other hand, velocity is a vector quantity; it is direction-aware. An object which moves in the negative direction has a negative velocity. If the object is slowing down then its acceleration vector is directed in the opposite direction as its motion in this case. Based on this we have to solve this question.

The diagram for the given question is given as:

$\mathrm{Y}+2 \mathrm{X}+\mathrm{Z}=\ell \quad \ldots(\mathrm{i})$
$\mathrm{Y}+\mathrm{X}+\ell_{2}+\mathrm{X}+\ell_{2}+\mathrm{Z}-\ell_{1}=\ell$
Subtracting eq.1 $^{\text {st }}$ from eq. $2^{\text {nd }}$, we get $2 \ell_{2}=\ell_{1}$
Differentiating twice this equation w.r.t time we get $\therefore \quad \mathrm{a}_{1}=2 \mathrm{a}_{2}$
i.e. acceleration of block $\mathrm{m}_{1}$ is twice the acceleration of block $\mathrm{m}_{2}$
For block $\mathrm{m}_{1}$
$\mathrm{T}_{1}=\mathrm{m}_{1} \mathrm{a}_{1}$
For block $\mathrm{m}_{2}$
$\mathrm{m}_{2} \mathrm{g}-\mathrm{T}_{2}=\mathrm{m}_{2} \mathrm{a}_{2}$
$2 \mathrm{T}_{1}=\mathrm{T}_{2} \quad[\because$ Pulley is massless]
Let $a_{2}=a \quad \because T=2 m_{1} a$
$\therefore a_{1}=2 a, m_{2} g-2 T=m_{2} a$
$T_{1}=T \quad$ Solving $a_{2}=\dfrac{m_{2} g}{m_{2}+4 m_{1}}$
$\therefore T_{2}=2 T \quad \therefore a_{1}=2 a_{2}=\dfrac{2 m_{2} g}{m_{2}+4 m_{1}}$
After we put the values, we get that:
$\begin{align}
  & {{a}_{1}}=2{{a}_{2}}=5 \\
 & \Rightarrow {{a}_{1}}=5,{{a}_{2}}=2.5 \\
\end{align}$

So, the correct answer is option A.

Note: We should know that if an object's speed or velocity is increasing at a constant rate then we say it has uniform acceleration. The rate of acceleration is constant. If a car speeds up then slows down then speeds up it doesn't have uniform acceleration. The instantaneous acceleration, or simply acceleration, is defined as the limit of the average acceleration when the interval of time considered approaches 0. It is also defined in a similar manner as the derivative of velocity with respect to time. If an object begins acceleration from rest or a standstill, its initial time is 0. If we get a negative value for acceleration, it means the object is slowing down. The acceleration of an object is its change in velocity over an increment of time. This can mean a change in the object's speed or direction. Average acceleration is the change of velocity over a period of time. Constant or uniform acceleration is when the velocity changes the same amount in every equal time period.