Question

Two blocks (A) and (B) are arranged on a smooth horizontal plane as shown in figure. If two forces of equal magnitude act on the block (A) and block (B). If the ratio of acceleration of block (A) to block (B) is $n:1$ (where n is an integer). Then find$n$. ($g = 10m/{s^2}$)

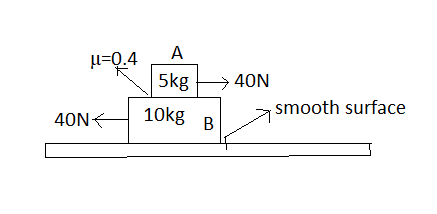
(A) $1$
(B) $2$
(C) $\dfrac{1}{2}$
(D) $0$

Answer 1

Hint To make it simpler to understand and solve this problem we first draw the free body diagrams of both the blocks (A) and (B) by isolating the blocks from one another. After drawing the free body diagrams of both the blocks we use friction formula and find the friction force acting on both the blocks. We add all the forces acting on each block and solve for acceleration. We then equate the ratio of acceleration given in the question to the actual ratio of acceleration in both the blocks to find n.
Formula used Friction force $f = \mu {F_N}$
Here,
Friction force is represented by $f$
Coefficient of friction is represented by $\mu $
Normal force is represented by ${F_N}$

Complete Step by step solution
Let us take block (A) first to solve
Free body diagram of block (A) is

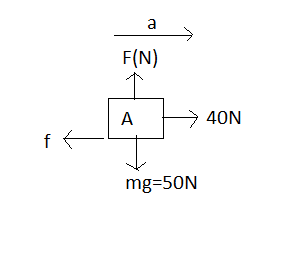
The normal force acting on block (A) is
${F_{N - A}} = {m_A}g = 50N$
From the formula of friction force
$f = \mu {F_{N - A}} = 0.4 \times 50 = 20N$
The sum of forces acting on block (A) in horizontal direction,
${m_A}{a_A} = 40 - f$
Acceleration of block (A) is
$ {a_A} = \dfrac{{40 - f}}{{{m_a}}} $
 $ {a_A} = \dfrac{{40 - 20}}{5} = 4m/{s^2} $
Here,
Friction force is represented by $f$
Normal force of (A) is represented by ${F_{N - A}}$
Mass of (A) is ${m_A}$
Acceleration of (A) is ${a_A}$
Taking block (B) under consideration
Friction force acting on block (B) will be the same as (A) because the friction force acting is between the surface of block (A) and block (B) with the weight of block (A) as the normal force.
${f_A} = {f_B} = f=20N$
The sum of all the forces acting on block (B) in the horizontal direction,
${m_B}{a_B} = 40 - f$
Acceleration of block (B) is equal to
${a_B} = \dfrac{{40 - f}}{{{m_B}}} $
$ {a_B} = \dfrac{{40 - 20}}{{10}} = 2m/{s^2} $
Here,
Friction force is represented by $f$
Mass of (B) is ${m_B}$
Acceleration of (B) is ${a_B}$
From the question ratio of accelerations is
$\dfrac{{{a_A}}}{{{a_B}}} = n:1 $
 $ \dfrac{{{a_A}}}{{{a_B}}} = \dfrac{4}{2} = \dfrac{2}{1} = \dfrac{n}{1} $
Hence $n$ is equal to $2$

Option (B) is the correct answer

Note There is no friction force between the surface of block (B) and the horizontal plane because the horizontal plane is smooth. Hence the friction force is zero between these two surfaces. The sign conventions taken in the above question are positive for right and upward directions, and negative for left and downward directions.