Question

Through the vertex of the parabola\[{{y}^{2}}=4x\]chords\[OP\]and\[OQ\]are drawn at
right angles to one another. The locus of middle point of\[PQ\]is
(a) \[{{y}^{2}}=x+8\]
(b) \[{{y}^{2}}=-2x+8\]
(c) \[{{y}^{2}}=2x-8\]
(d) \[{{y}^{2}}=x-8\]

Answer 1

Hint: To find the locus of the middle point of two points on the parabola, write the points in parametric form and then find the middle point of the points. Use the fact that the product of slope of any two perpendicular lines is\[-1\].

We have the parabola\[{{y}^{2}}=4x\]. We want to find the locus of middle point of two
points on the parabola such that the chords joining two points of the parabola to its vertex are
perpendicular to each other.
We know that the vertex of parabola of the form\[{{y}^{2}}=4ax\]is\[\left( 0,0 \right)\].
Thus, we have\[\left( 0,0 \right)\]as the vertex of the parabola\[{{y}^{2}}=4x\].


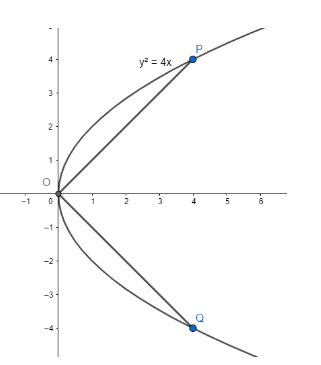
To find the locus of middle point of\[PQ\], let’s write the points in parametric form.
We know that any point of the parabola\[{{y}^{2}}=4ax\] is of the form\[\left( a{{t}^{2}},2at \right)\].
Substituting\[a=1\]in the above equation, we have the two points on our parabola as\[P\left(
{{t}_{1}} \right)=\left( t_{1}^{2},2{{t}_{1}} \right)\]and\[Q\left( {{t}_{2}} \right)=\left(
t_{2}^{2},2{{t}_{2}} \right)\].
We know that the equation of any line passing through origin is of the form\[y=mx\].
Let’s assume that the equation of line joining origin and\[P\left( {{t}_{1}} \right)=\left(
t_{1}^{2},2{{t}_{1}} \right)\]is of the form\[y={{m}_{1}}x\].
Substituting the point\[P\left( {{t}_{1}} \right)=\left( t_{1}^{2},2{{t}_{1}} \right)\]in the equation of
line, we have\[2{{t}_{1}}={{m}_{1}}t_{1}^{2}\].
Thus, we have\[{{m}_{1}}=\dfrac{2}{{{t}_{1}}}\]. \[...\left( 1 \right)\]
Let’s assume that the equation of line joining origin and\[Q\left( {{t}_{2}} \right)=\left(
t_{2}^{2},2{{t}_{2}} \right)\]is of the form\[y={{m}_{2}}x\].
Substituting the point\[Q\left( {{t}_{2}} \right)=\left( t_{2}^{2},2{{t}_{2}} \right)\]in the equation of
line, we have\[2{{t}_{2}}={{m}_{2}}t_{2}^{2}\].
Thus, we have\[{{m}_{2}}=\dfrac{2}{{{t}_{2}}}\]. \[...\left( 2 \right)\]
We know that the two chords passing through\[P\]and\[Q\]are perpendicular, so the product of
their slope is\[-1\].
Using equation\[\left( 1 \right)\]and\[\left( 2 \right)\], we have\[{{m}_{1}}{{m}_{2}}=-1\].
\[\begin{align}
& \Rightarrow \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\
& \Rightarrow {{t}_{1}}{{t}_{2}}=-4 \\
\end{align}\]

Thus, we can write\[{{t}_{1}}\]as\[{{t}_{1}}=\dfrac{-4}{{{t}_{2}}}\]. \[...\left( 3 \right)\]
We know that the middle point of two points of the form\[\left( {{x}_{1}},{{y}_{1}} \right)\]and\[\left(
{{x}_{2}},{{y}_{2}} \right)\]is\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\].
Substituting\[{{x}_{1}}=t_{1}^{2},{{y}_{1}}=2{{t}_{1}},{{x}_{2}}=t_{2}^{2},{{y}_{2}}=2{{t}_{2}}\]in the
above equation, we have\[\left( \dfrac{t_{1}^{2}+t_{2}^{2}}{2},\dfrac{2{{t}_{1}}+2{{t}_{2}}}{2}
\right)\]as the mid point of the points\[P\left( {{t}_{1}} \right)\]and\[Q\left( {{t}_{2}} \right)\].
Let’s assume\[x=\dfrac{t_{1}^{2}+t_{2}^{2}}{2},y=\dfrac{2{{t}_{1}}+2{{t}_{2}}}{2}\].
Substituting equation\[\left( 3 \right)\]in the above equation, we have\[x=\dfrac{{{\left( \dfrac{-
4}{{{t}_{2}}} \right)}^{2}}+t_{2}^{2}}{2},y=\dfrac{2\left( \dfrac{-4}{{{t}_{2}}} \right)+2{{t}_{2}}}{2}\].
Solving the above equation, we get\[x=\dfrac{{{\left( \dfrac{-4}{{{t}_{2}}}
\right)}^{2}}+t_{2}^{2}}{2}\]and\[y=\dfrac{-4}{{{t}_{2}}}+{{t}_{2}}\].
Squaring the second equation, we get\[{{y}^{2}}={{\left( \dfrac{-4}{{{t}_{2}}} \right)}^{2}}+t_{2}^{2}-
8\].
\[\Rightarrow {{y}^{2}}+8={{\left( \dfrac{-4}{{{t}_{2}}} \right)}^{2}}+t_{2}^{2}\]
Substituting the above equation in\[x=\dfrac{{{\left( \dfrac{-4}{{{t}_{2}}} \right)}^{2}}+t_{2}^{2}}{2}\],
we get\[x=\dfrac{{{\left( \dfrac{-4}{{{t}_{2}}} \right)}^{2}}+t_{2}^{2}}{2}=\dfrac{{{y}^{2}}+8}{2}\].
\[\Rightarrow 2x={{y}^{2}}+8\]
Hence, the correct answer is\[{{y}^{2}}=2x-8\].

Note: It’s necessary to use the fact that the two chords are perpendicular and hence, the product of their slope is\[-1\].