Question

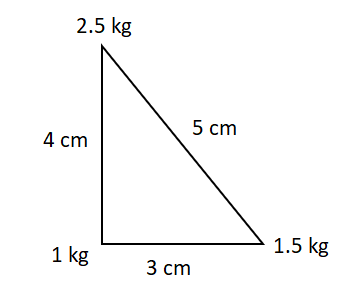
Three point particles of mass 1 kg, 1.5 kg and 2.5 kg are placed at three corners of a right triangle of sides 4.0 cm, 3.0 cm and 5.0 cm as shown in the figure. The centre of mass of the system is at the point:
A. 0.9 cm right and 2.0 cm above 1 kg mass
B. 2.0 cm right and 0.9 cm above 1 kg mass
C. 1.5 cm right and 1.2 cm above 1 kg mass
D. 0.6 cm right and 2.0 cm above 1 kg mass

Answer 1

Hint:To solve this problem, we need to use a formula for the effective centre of mass of the system at a given point. In this question we have a system of 3 particles present on 3 corners of a right triangle, so the centre of mass will lie somewhere between them.




Formula used:
The centre of mass is given as,
Along X coordinate \[{X_{COM}} = \dfrac{{\sum {{m_i}{x_i}} }}{{\sum {{m_i}} }}\]
Along Y coordinate \[{Y_{COM}} = \dfrac{{\sum {{m_i}{y_i}} }}{{\sum {{m_i}} }}\]





Complete answer:
Given (0,0), (3,0) and (0,4) to be the coordinates of mass 1kg, 1.5kg and 2.5kg by assuming 1kg at origin.

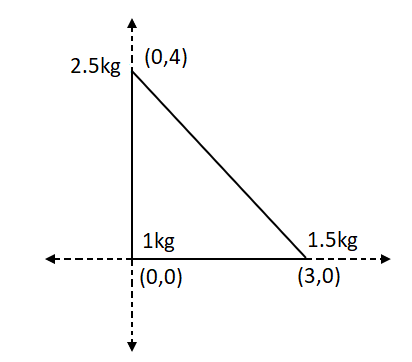
Image: Three point particles are placed at three corners of a right triangle.

\[{X_{COM}}\] can be given as,
\[{X_{COM}} = \dfrac{{\sum {{m_i}{x_i}} }}{{\sum {{m_i}} }}\]
\[{X_{COM}} = \dfrac{{1 \times 0 + 1.5 \times 3 + 2.5 \times 0}}{{1 + 1.5 + 2.5}}\]
          \[ = \dfrac{{4.5}}{5} = 0.9cm\]
\[{Y_{COM}}\] can be given as,
\[{Y_{COM}} = \dfrac{{\sum {{m_i}{y_i}} }}{{\sum {{m_i}} }}\]
\[{Y_{COM}} = \dfrac{{1 \times 0 + 1.5 \times 0 + 2.5 \times 4}}{{1 + 1.5 + 2.5}}\]
          \[ = \dfrac{4}{2} = 2cm\]
Therefore, the centre of mass is 0.9 cm to the right and 2 cm above the mass of 1kg.
Hence option A is the correct answer






Note: We use the formula for centre of mass for individual coordinates in the x-y-z plane which is only applicable for point objects, for an extended object or non-uniform object like a rod, we need to consider differential mass and its position and integrate over its entire length.