Question

Three identical particles each of mass $m$ are placed at the corners of the equilateral triangle at side $a$. Find the gravitational force exerted on one body due to the other two.

Answer 1

Hint: We have an equilateral triangle whose all angles are equal to $60^\circ $ . We have to use the formula of gravitational force which is equal to $\overrightarrow F = G\dfrac{{Mm}}{{{r^2}}}$. After that for net force add both the forces which act on it due to both sides.

Complete step by step solution:
We have an equilateral triangle whose all sides are equal and angles are of $60^\circ $. Now let $L = a$ be the side of a triangle.

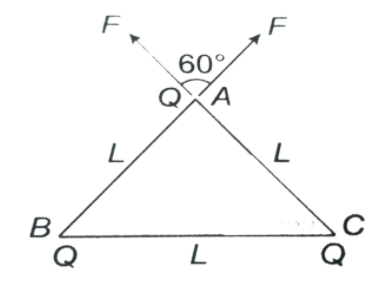
Here all the particles are of the same mass as $m$.
We will use Newton's laws to solve this question. Newton's law of universal gravitation says that every particle attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Therefore,
$\overrightarrow F = G\dfrac{{Mm}}{{{r^2}}}$
Now put the values, calculate magnitude of force due to particle B, we get
${\overrightarrow F _1} = G\dfrac{{{m^2}}}{{{r^2}}}$
Now calculate magnitude of force due to particle C, we get
${\overrightarrow F _2} = G\dfrac{{{m^2}}}{{{r^2}}}$
Now, we are given that both the forces are at $60^\circ $ . Therefore net force is equal to
$\overrightarrow {{F_{net}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} $
And the magnitude of this net force will be
$ \Rightarrow \sqrt {{F^2}_1 + {F_2}^2 + 2{F_1}{F_2}\cos 60°} $
After putting the value of $\cos 60$ , we get
$ \Rightarrow \sqrt {{F^2} + {F^2} + 2{F^2} \times \dfrac{1}{2}}$ (since $\cos 60° = \dfrac{1}{2}$ )
$ \Rightarrow \sqrt {3{F^2}} $
Hence, we get the net force equal to
${F_{net}} = \sqrt 3 F$
And lastly put value of $F$ to get the final answer
${F_{net}} = \sqrt 3 G\dfrac{{{m^2}}}{{{r^2}}}$
This is the value asked in the question.

Note: Always remember about the units of quantities. Here, the mass of all the particles is the same so refer to them with the same name and also remember that force is a vector quantity so direction matters.