Answer
64.8k+ views
Hint: The given charges are kept at the vertices A, B and c respectively of an equilateral triangle ABC of \[10cm\]. Also we have to find the resultant force on the charge at the vertex C.
Consider a closed ABC triangle, and C will take a force on the charge. The diagram shown below.
Complete step by step answer:
The diagram will be like this,
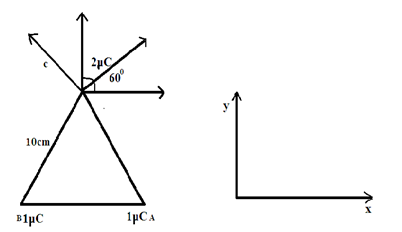
An equiangular triangle has three equal sides and angles. It will always have an angle of ${60^ \circ }$ in each corner.
Component of force due to B and A in x direction acting on C cancel out each other
\[\therefore {F_x} = 0\]
In $y$ direction forces add up
We get ${F_x} = \dfrac{{k(1\mu C)(2\mu C)}}{{{{(10 \times {{10}^{ - 2}})}^2}}} \times \sin 60 \times 2$
Substitute the values, and $\sin 60 = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \dfrac{{9 \times {{10}^9} \times 1 \times {{10}^{ - 6}} \times 2 \times {{10}^{ - 6}}}}{{100 \times {{10}^{ - 6}}}} \times \dfrac{{\sqrt 3 }}{2} \times 2$
Cancelling the same term and multiply to the remaining terms, we get
So we get,
$ \Rightarrow 3.1176N$
So, The correct answer is option (D).
Additional information:
In geometry, a triangle may be a closed, two-dimensional shape with three straight sides. A triangle is also a polygon. A triangle with all sides equilateral, a triangle with two sides equal is called isosceles, and a triangle with all sides a different length is called scalene.
Note: Triangles are often broadly classified into two types, which are:
Triangle based on the lengths of their sides
A) According to the lengths of their sides, triangles can be classified into three types with are:
i) Scalene
ii) Isosceles
iii) Equilateral
Triangles based on the their interior angles
B) According to the their interior angles, triangles can be classified into three types with are:
i) Acute-angled
ii) Obtuse-angled
iii) Right-angled
Consider a closed ABC triangle, and C will take a force on the charge. The diagram shown below.
Complete step by step answer:
The diagram will be like this,

An equiangular triangle has three equal sides and angles. It will always have an angle of ${60^ \circ }$ in each corner.
Component of force due to B and A in x direction acting on C cancel out each other
\[\therefore {F_x} = 0\]
In $y$ direction forces add up
We get ${F_x} = \dfrac{{k(1\mu C)(2\mu C)}}{{{{(10 \times {{10}^{ - 2}})}^2}}} \times \sin 60 \times 2$
Substitute the values, and $\sin 60 = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \dfrac{{9 \times {{10}^9} \times 1 \times {{10}^{ - 6}} \times 2 \times {{10}^{ - 6}}}}{{100 \times {{10}^{ - 6}}}} \times \dfrac{{\sqrt 3 }}{2} \times 2$
Cancelling the same term and multiply to the remaining terms, we get
So we get,
$ \Rightarrow 3.1176N$
So, The correct answer is option (D).
Additional information:
In geometry, a triangle may be a closed, two-dimensional shape with three straight sides. A triangle is also a polygon. A triangle with all sides equilateral, a triangle with two sides equal is called isosceles, and a triangle with all sides a different length is called scalene.
Note: Triangles are often broadly classified into two types, which are:
Triangle based on the lengths of their sides
A) According to the lengths of their sides, triangles can be classified into three types with are:
i) Scalene
ii) Isosceles
iii) Equilateral
Triangles based on the their interior angles
B) According to the their interior angles, triangles can be classified into three types with are:
i) Acute-angled
ii) Obtuse-angled
iii) Right-angled
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

What is the common property of the oxides CONO and class 10 chemistry JEE_Main

What happens when dilute hydrochloric acid is added class 10 chemistry JEE_Main

If four points A63B 35C4 2 and Dx3x are given in such class 10 maths JEE_Main

The area of square inscribed in a circle of diameter class 10 maths JEE_Main

Other Pages
A boat takes 2 hours to go 8 km and come back to a class 11 physics JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

In the ground state an element has 13 electrons in class 11 chemistry JEE_Main

According to classical free electron theory A There class 11 physics JEE_Main

Differentiate between homogeneous and heterogeneous class 12 chemistry JEE_Main

Excluding stoppages the speed of a bus is 54 kmph and class 11 maths JEE_Main



