Question

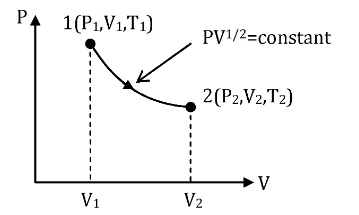
Thermodynamic process is shown below on a P-V diagram for one mole of an ideal gas. If V2 = 2V1 then the ratio of temperature T2/T1 is:

Answer 1

Hint: The above diagram represents how the pressure, volume and temperature of the ideal gas vary when going from state 1 to state 2. The relation between pressure and volume is given in the diagram. Since the system consists of an ideal gas, the ideal gas equation holds good. Equating the two relations should give you the answer.

Complete Step by Step Solution:
The P-V diagram shown above represents the change in pressure (P), volume (V) and temperature (T) when the given system of one mole of an ideal gas moves from state 1 to state 2. It is also given that during the process, pressure and volume obey the relation \[P{V^{1/2}} = \]constant (\[k\]) … (1)
We are required to calculate \[\dfrac{{{T_2}}}{{{T_1}}}\] if volumes V1 and V2 were related as \[{V_2} = 2{V_1}\] … (2)
Since the system consists of one mole of an ideal gas, the ideal gas equation \[PV = nRT\]holds good in this case where \[n = 1\]. Thus, the ideal gas equation becomes \[PV = RT\] … (3)
where R is the gas constant.

Equation (3) can be rewritten as \[PV = RT \Rightarrow T = \dfrac{{PV}}{R}\]
\[ \Rightarrow T = \dfrac{{P\sqrt V \times \sqrt V }}{R}\]
\[ \Rightarrow T = \dfrac{{k\sqrt V }}{R}\] [from equation (1)] … (4)

For states 1 and 2, equation (4) becomes \[{T_1} = \dfrac{{k\sqrt {{V_1}} }}{R}\] and \[{T_2} = \dfrac{{k\sqrt {{V_2}} }}{R}\]respectively.
Thus, \[\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\left( {\dfrac{{k\sqrt {{V_1}} }}{R}} \right)}}{{\left( {\dfrac{{k\sqrt {{V_2}} }}{R}} \right)}}\]
\[ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\sqrt {{V_1}} }}{{\sqrt {{V_2}} }}\]
\[ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\sqrt {{V_1}} }}{{\sqrt {2{V_1}} }}\] [from equation (2)]
\[ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{{\sqrt 2 }}\]
\[ \Rightarrow \dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{\sqrt 2 }}{1}\]

Thus, the ratio \[\dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{\sqrt 2 }}{1}\] if V₂=2V₁.

Note: In this process, since there is an increase in volume and a decrease in pressure, the process is an expansion process. Here, pressure and volume obey the general relation \[P{V^\gamma } = \] constant thus, the process can be considered to be an adiabatic expansion.