
The variation of the acceleration a of the particle executing S.H.M.with displacement x is as shown in the figure
A. 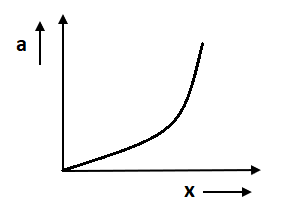
B. 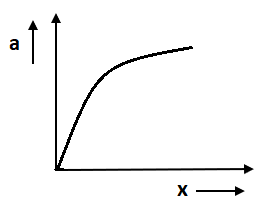
C. 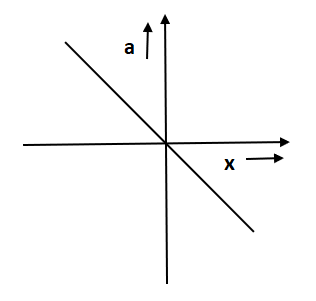
D. 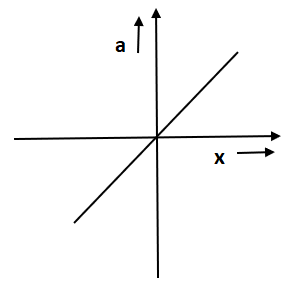
Answer
217.5k+ views
Hint: Here the graph is given between acceleration(a) and displacement(x). So, to find the correct graph we need to use the relation between acceleration and displacement in simple harmonic motion. By using the relation between the acceleration and the displacement of the SHM we can easily draw the graph between them.
Formula used:
The acceleration (a) of the particle executing simple harmonic motion (SHM) is given as,
\[a = - {\omega ^2}A\sin (\omega t + \phi )\]
\[\Rightarrow a = - {\omega ^2}x\]
Where \[\omega \] is angular frequency, A is the amplitude, t is the time taken, \[\phi \] is the phase constant and x is the displacement.
Complete step by step solution:
As we know that the displacement x in simple harmonic motion (SHM) is given as,
\[x = A\sin (\omega t + \phi ) \\ \]
Also, the acceleration a of the particle executing simple harmonic motion (SHM) is given as,
\[a = - {\omega ^2}A\sin (\omega t + \phi ) \\ \]
Now the acceleration(a) of the particle which is related to the displacement (x) executing a simple harmonic motion (SHM) is
\[a = - {\omega ^2}x \\ \]
Here acceleration a and displacement x are linearly dependent on each other.
This equation shows the straight-line equation passing through origin as,
\[y = mx + c \\ \]
So, after comparing both we get a negative slope. In option C and D a straight line is given. In option D slope is positive as the angle is positive whereas in option C slope is negative.
Hence option C is the correct answer.
Note: Simple Harmonic Motion (SHM) is defined as a motion in which the restoring force(F) is directly proportional to the displacement(x) of the body from its mean position or equilibrium position. It can also be known as an oscillatory motion in which the acceleration of the body at any position is directly proportional to the displacement which is from the mean position.
Formula used:
The acceleration (a) of the particle executing simple harmonic motion (SHM) is given as,
\[a = - {\omega ^2}A\sin (\omega t + \phi )\]
\[\Rightarrow a = - {\omega ^2}x\]
Where \[\omega \] is angular frequency, A is the amplitude, t is the time taken, \[\phi \] is the phase constant and x is the displacement.
Complete step by step solution:
As we know that the displacement x in simple harmonic motion (SHM) is given as,
\[x = A\sin (\omega t + \phi ) \\ \]
Also, the acceleration a of the particle executing simple harmonic motion (SHM) is given as,
\[a = - {\omega ^2}A\sin (\omega t + \phi ) \\ \]
Now the acceleration(a) of the particle which is related to the displacement (x) executing a simple harmonic motion (SHM) is
\[a = - {\omega ^2}x \\ \]
Here acceleration a and displacement x are linearly dependent on each other.
This equation shows the straight-line equation passing through origin as,
\[y = mx + c \\ \]
So, after comparing both we get a negative slope. In option C and D a straight line is given. In option D slope is positive as the angle is positive whereas in option C slope is negative.
Hence option C is the correct answer.
Note: Simple Harmonic Motion (SHM) is defined as a motion in which the restoring force(F) is directly proportional to the displacement(x) of the body from its mean position or equilibrium position. It can also be known as an oscillatory motion in which the acceleration of the body at any position is directly proportional to the displacement which is from the mean position.
Recently Updated Pages
Addition of Three Vectors: Methods & Examples

Addition of Vectors: Simple Guide for Students

Algebra Made Easy: Step-by-Step Guide for Students

Relations and Functions: Complete Guide for Students

Analytical Method of Vector Addition Explained Simply

Arithmetic, Geometric & Harmonic Progressions Explained

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




