Question

The tube shows a pipe of uniform cross-section inclined in a vertical plane. A U-tube manometer is connected between the points A and B. If the liquid of density \[{{\rho }_{0}}\] flows with velocity \[{{v}_{0}}\] in the pipe, then the reading \[h\] of the manometer is

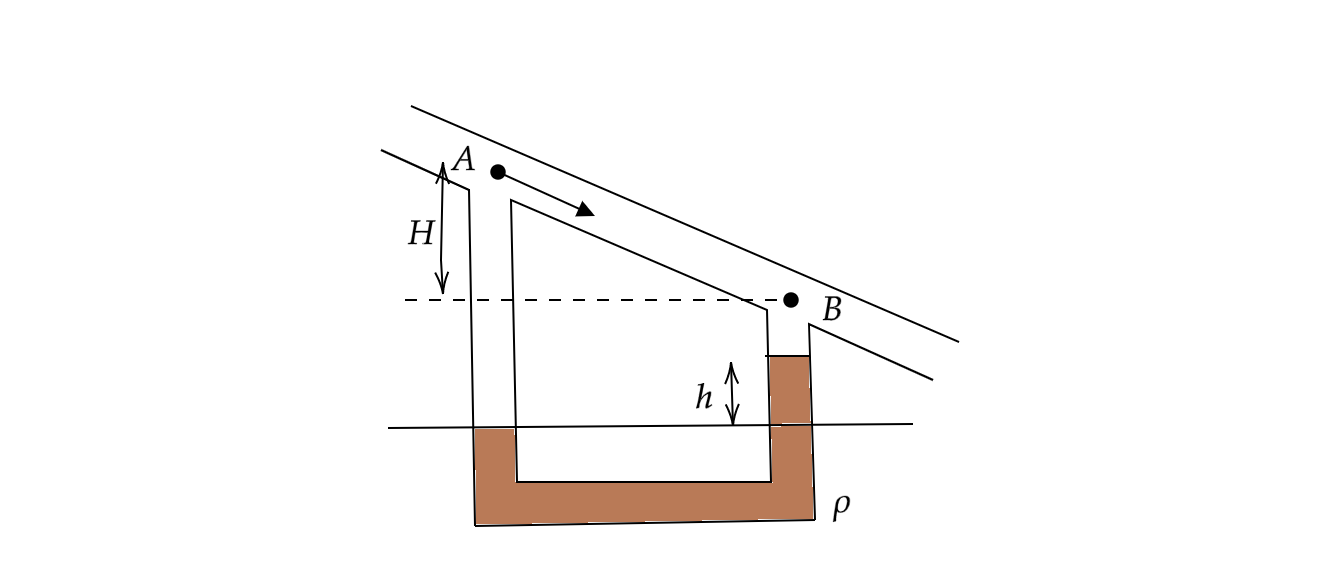
(A) \[h=0\]
(B) \[h=\dfrac{{{v}_{0}}^{2}}{2g}\]
(C) \[h=\dfrac{{{\rho }_{0}}}{\rho }\left( \dfrac{{{v}_{0}}^{2}}{2g} \right)\]
(D) \[h=\dfrac{{{\rho }_{0}}H}{\rho -{{\rho }_{0}}}\]

Answer 1

Hint: Manometers are pressure measuring devices that use liquid columns in vertical or inclined planes. We have to find the height of the liquid column. For that, we must know the pressure acting at point B. We can find the velocity at B using the continuity equation and then proceed with Bernoulli’s equation to find the pressure.


Formula Used:
\[{{\rho }_{A}}\times {{v}_{A}}={{\rho }_{B}}\times {{v}_{A}}\]
\[{{P}_{1}}+\rho g{{h}_{1}}+\dfrac{1}{2}\rho {{v}_{1}}^{2}={{P}_{2}}+\rho g{{h}_{2}}+\dfrac{1}{2}\rho {{v}_{2}}^{2}\]
\[\Delta P=\rho gh\]

Complete step by step answer:
From the continuity equation of fluids, we know that mass of liquid flowing in a tube must equal the mass flowing out. Mass is a product of density and volume. Hence the product of the density and the volume at points A and B must be the same. Since density is the same at both points, hence the volume of water flowing per unit time through both these points must be same. And since the area of cross-section of the tube is uniform, the velocity at point A must be equal to the velocity at point B.
 Mathematically, we can depict it using the continuity equation
\[\begin{align}
  & {{\rho }_{A}}\times {{v}_{A}}={{\rho }_{B}}\times {{v}_{B}} \\
 & \Rightarrow {{v}_{A}}={{v}_{B}}(\because {{\rho }_{A}}={{\rho }_{B}}) \\
\end{align}\]

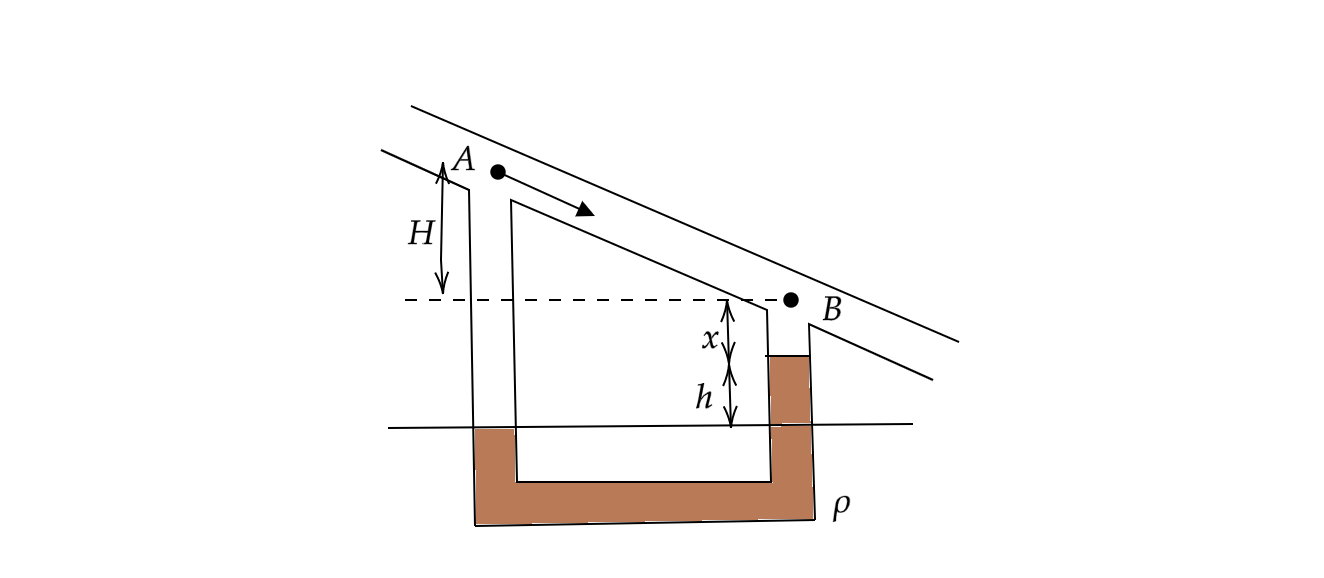
Applying Bernoulli’s theorem at points A and B, we get
\[\begin{align}
  & {{P}_{A}}+{{\rho }_{0}}g(H+h+x)={{P}_{B}}+{{\rho }_{0}}gx+\rho gh \\
 & \Rightarrow h({{\rho }_{0}}-\rho )g=({{P}_{B}}-{{P}_{A}})+{{\rho }_{0}}gH \\
 & \Rightarrow h=\dfrac{({{P}_{B}}-{{P}_{A}})-{{\rho }_{0}}gH}{({{\rho }_{0}}-\rho )g}--equation(1) \\
\end{align}\]
Equating the pressure along the dotted line, we get
\[\begin{align}
  & {{P}_{A}}+{{\rho }_{0}}gH={{P}_{B}} \\
 & \Rightarrow ({{P}_{B}}-{{P}_{A}})={{\rho }_{0}}gH--equation(2) \\
\end{align}\]
From the two equations obtained above, we can say that
\[\begin{align}
  & \Rightarrow h=\dfrac{{{\rho }_{0}}gH-{{\rho }_{0}}gH}{({{\rho }_{0}}-\rho )g} \\
 & \Rightarrow h=0 \\
\end{align}\]

Hence option (A) is the correct answer.

Note: If the cross-section of the pipe was non-uniform, then we would have to make changes in our continuity equation. Also, note that Bernoulli’s theorem has a term that is equal to the product of the density of the liquid and the square of the velocity. We’ve neglected that term because the density and the velocity of the liquid are the same at both the points, hence we could neglect it.