
The temperature inside & outside of the refrigerator is 260 K and 315 K respectively. Assuming that the refrigerator cycle is reversible, calculate the heat delivered to the surrounding for every joule of work done.
Answer
217.8k+ views
Hint Here, we are given the inside and outside temperature of a refrigerator. The inside of a refrigerator should be treated as a sink and the outside of the refrigerator should be taken as the source. We need to find the amount of heat delivered per unit work done. For that we first need to find the amount of heat extracted from the fridge per unit work.
Complete step by step solution
The reversible refrigeration cycle is the ideal reverse Carnot cycle or Carnot refrigeration cycle. A Carnot refrigerator is a device that removes heat \[\left( {{Q_2}} \right)\] from the low temperature source or the inside of the refrigerator \[\left( {{T_2}} \right)\] to a higher temperature \[\left( {{T_1}} \right)\] sink or the outside of the refrigerator by using mechanical work (W).
Where \[{Q_1}\] is the heat delivered to the surroundings
and \[{Q_2}\] is the heat extracted from the refrigerator
The work done by the refrigerator, $W = {Q_2} - {Q_1}$.
Now, the coefficient of performance of a Carnot refrigerator is given by:
\[\beta = \dfrac{{{Q_2}}}{W} = \dfrac{{{T_2}}}{{{T_2} - {T_1}}}\] ---- (1)
Where, \[{T_2}\] is the temperature of the refrigerator, i.e. inside of the refrigerator
\[{T_1}\] is the temperature of the surroundings, i.e. outside of the refrigerator
In the question, we are given \[{T_1}\] = 315 K and \[{T_2}\] = 260 K. Putting these values in equation (1),
$
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{{T_2}}}{{{T_2} - {T_1}}} \\
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{260}}{{315 - 260}} \\
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{260}}{{55}} \\
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{52}}{{11}} \\
$
Now, we have to find the heat delivered to the surrounding for every joule of work done. For this we will take work done, $W = 1J$.
$
\Rightarrow \dfrac{{{Q_2}}}{1} = \dfrac{{52}}{{11}} \\
\Rightarrow {Q_2} = 4.72727 \\
\Rightarrow {Q_2} \approx 4.73 \\
$
This is the heat extracted from the refrigerator per joule of work done. We need to find the heat delivered to the surroundings for every 1J of work done, i.e. we need to find \[{Q_1}\] for \[W = 1J\].
$
\because W = {Q_2} - {Q_1} \\
\Rightarrow {Q_1} = {Q_2} + W \\
\Rightarrow {Q_1} = 4.73 + 1 \\
\Rightarrow {Q_1} = 5.73 \\
$
Therefore, the heat delivered to the surrounding for every joule of work done will be 5.73 J.
Note: Here is the basic diagram for the given reversible /carnot refrigerator for better understanding of the problem :
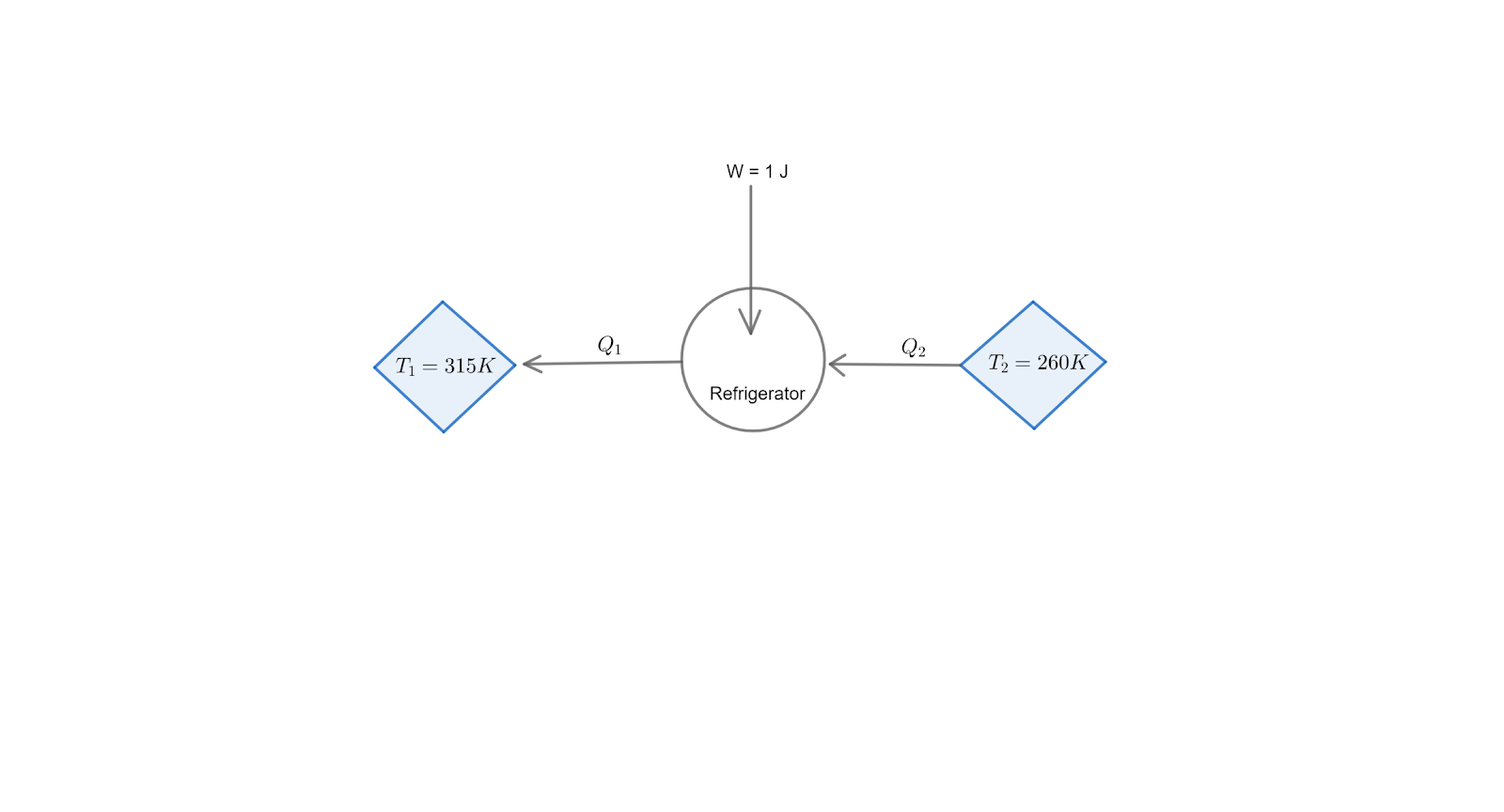
Complete step by step solution
The reversible refrigeration cycle is the ideal reverse Carnot cycle or Carnot refrigeration cycle. A Carnot refrigerator is a device that removes heat \[\left( {{Q_2}} \right)\] from the low temperature source or the inside of the refrigerator \[\left( {{T_2}} \right)\] to a higher temperature \[\left( {{T_1}} \right)\] sink or the outside of the refrigerator by using mechanical work (W).
Where \[{Q_1}\] is the heat delivered to the surroundings
and \[{Q_2}\] is the heat extracted from the refrigerator
The work done by the refrigerator, $W = {Q_2} - {Q_1}$.
Now, the coefficient of performance of a Carnot refrigerator is given by:
\[\beta = \dfrac{{{Q_2}}}{W} = \dfrac{{{T_2}}}{{{T_2} - {T_1}}}\] ---- (1)
Where, \[{T_2}\] is the temperature of the refrigerator, i.e. inside of the refrigerator
\[{T_1}\] is the temperature of the surroundings, i.e. outside of the refrigerator
In the question, we are given \[{T_1}\] = 315 K and \[{T_2}\] = 260 K. Putting these values in equation (1),
$
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{{T_2}}}{{{T_2} - {T_1}}} \\
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{260}}{{315 - 260}} \\
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{260}}{{55}} \\
\Rightarrow \dfrac{{{Q_2}}}{W} = \dfrac{{52}}{{11}} \\
$
Now, we have to find the heat delivered to the surrounding for every joule of work done. For this we will take work done, $W = 1J$.
$
\Rightarrow \dfrac{{{Q_2}}}{1} = \dfrac{{52}}{{11}} \\
\Rightarrow {Q_2} = 4.72727 \\
\Rightarrow {Q_2} \approx 4.73 \\
$
This is the heat extracted from the refrigerator per joule of work done. We need to find the heat delivered to the surroundings for every 1J of work done, i.e. we need to find \[{Q_1}\] for \[W = 1J\].
$
\because W = {Q_2} - {Q_1} \\
\Rightarrow {Q_1} = {Q_2} + W \\
\Rightarrow {Q_1} = 4.73 + 1 \\
\Rightarrow {Q_1} = 5.73 \\
$
Therefore, the heat delivered to the surrounding for every joule of work done will be 5.73 J.
Note: Here is the basic diagram for the given reversible /carnot refrigerator for better understanding of the problem :

Recently Updated Pages
Arithmetic, Geometric & Harmonic Progressions Explained

Cartesian Form of Vector Explained: Formula, Examples & Uses

Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

How to Convert a Galvanometer into an Ammeter or Voltmeter




