
The slope of the tangent to a curve $y = f\left( x \right)$ at $\left( {x,f\left( x \right)} \right)$ is $2x + 1$ . If the curve passes through the point $\left( {1,2} \right)$ , then what is the area of the region bounded by the curve, the x-axis and the line $x = 1$ ?
A. $\dfrac{5}{6}$ sq. unit
B. $\dfrac{6}{5}$ sq. unit
C. $\dfrac{1}{6}$ sq. unit
D. $6$ sq. unit
Answer
218.4k+ views
Hint:In the above question, we are provided with the equation of the tangent to the curve. We are also provided with a point through which the curve is passing. Use this to evaluate the equation of the curve. Then, proceed further to calculate the area enclosed within the curve, the line, and the x-axis using integration.
Formula used: Area under a curve $y = f\left( x \right)$ , above x-axis, between two points $x = a$ and $x = b$ is calculated as $A = \int_a^b {f\left( x \right)dx} $ .
Complete step by step Solution:
The equation of the tangent to a curve $y = f\left( x \right)$ at a point is $y = 2x + 1$ .
Therefore,
$f'\left( x \right) = 2x + 1$
Integrating both sides with respect to $x$,
$f\left( x \right) = \int {f'\left( x \right)dx = \int {\left( {2x + 1} \right)dx} } $
Integrating,
$f\left( x \right) = {x^2} + x + c$
It is also given that the curve passes through $\left( {1,2} \right)$ , therefore,
$2 = f\left( 1 \right) = {\left( 1 \right)^2} + 1 + c$
Thus, $c = 0$ .
Hence, the equation of the curve is $f\left( x \right) = {x^2} + x$ .
The line $x = 1$ will intersect this curve at $\left( {1,2} \right)$ .
Let us plot the curves and the line and shade the enclosed area.
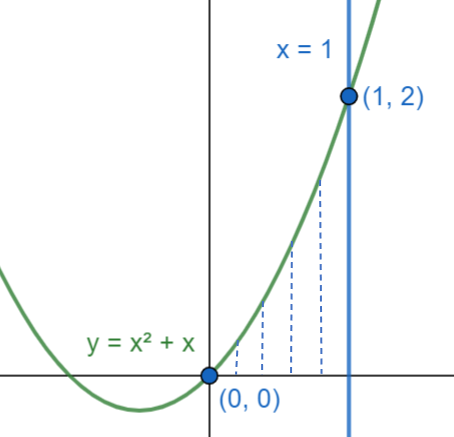
Clearly, the area enclosed in the area under the curve $y = {x^2} + x$ from $x = 0$ to $x = 1$ .
Hence, the enclosed area is calculated as:
$\int_0^1 {\left( {{x^2} + x} \right)dx} $
Integrating,
$\int_0^1 {\left( {{x^2} + x} \right)dx} = \left[ {\dfrac{{{x^3}}}{3} + \dfrac{{{x^2}}}{2}} \right]_0^1$
Calculating the definite integral,
$\int_0^1 {\left( {{x^2} + x} \right)dx} = \dfrac{1}{3} + \dfrac{1}{2} = \dfrac{5}{6}$
Thus, enclosed within the curve, the line $x = 1$ and the x-axis is $\dfrac{5}{6}$ sq. units.
Therefore, the correct option is (A).
Note:The slope of the tangent of a curve at a particular point gives the value of its derivative at that point. Thus, the equation of the tangent gives the equation of the first derivative of that curve.
Formula used: Area under a curve $y = f\left( x \right)$ , above x-axis, between two points $x = a$ and $x = b$ is calculated as $A = \int_a^b {f\left( x \right)dx} $ .
Complete step by step Solution:
The equation of the tangent to a curve $y = f\left( x \right)$ at a point is $y = 2x + 1$ .
Therefore,
$f'\left( x \right) = 2x + 1$
Integrating both sides with respect to $x$,
$f\left( x \right) = \int {f'\left( x \right)dx = \int {\left( {2x + 1} \right)dx} } $
Integrating,
$f\left( x \right) = {x^2} + x + c$
It is also given that the curve passes through $\left( {1,2} \right)$ , therefore,
$2 = f\left( 1 \right) = {\left( 1 \right)^2} + 1 + c$
Thus, $c = 0$ .
Hence, the equation of the curve is $f\left( x \right) = {x^2} + x$ .
The line $x = 1$ will intersect this curve at $\left( {1,2} \right)$ .
Let us plot the curves and the line and shade the enclosed area.

Clearly, the area enclosed in the area under the curve $y = {x^2} + x$ from $x = 0$ to $x = 1$ .
Hence, the enclosed area is calculated as:
$\int_0^1 {\left( {{x^2} + x} \right)dx} $
Integrating,
$\int_0^1 {\left( {{x^2} + x} \right)dx} = \left[ {\dfrac{{{x^3}}}{3} + \dfrac{{{x^2}}}{2}} \right]_0^1$
Calculating the definite integral,
$\int_0^1 {\left( {{x^2} + x} \right)dx} = \dfrac{1}{3} + \dfrac{1}{2} = \dfrac{5}{6}$
Thus, enclosed within the curve, the line $x = 1$ and the x-axis is $\dfrac{5}{6}$ sq. units.
Therefore, the correct option is (A).
Note:The slope of the tangent of a curve at a particular point gives the value of its derivative at that point. Thus, the equation of the tangent gives the equation of the first derivative of that curve.
Recently Updated Pages
In a game two players A and B take turns in throwing class 12 maths JEE_Main

The number of ways in which 6 men and 5 women can dine class 12 maths JEE_Main

The area of an expanding rectangle is increasing at class 12 maths JEE_Main

If y xxx cdots infty then find dfracdydx A yxy 1 B class 12 maths JEE_Main

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance




