Question

The shortest height of a vertical mirror required to see the entire image of a man, will be.
(A) One-third the man's height
(B) Half the man's height
(C) Two-third the man's height
(D) Data insufficient

Answer 1

Hint: We know that for a thin lens in air, the focal length is the distance from the center of the lens to the principal foci (or focal points) of the lens. For a converging lens (for example a convex lens), the focal length is positive, and is the distance at which a beam of collimated light will be focused to a single spot. The focal length of the lens is the distance between the lens and the image sensor when the subject is in focus, usually stated in millimetres (e.g., 28 mm, 50 mm, or 100 mm). In the case of zoom lenses, both the minimum and maximum focal lengths are stated, for example 18–55 mm.

Complete step by step answer
The diagram for the question is given below:

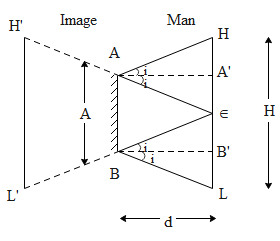
Here, $\tan {{i}_{1}}=\dfrac{{{A}^{\backslash }}E}{d}$
and we can say that $\tan {{i}_{1}}=\dfrac{{{A}^{\backslash }}H}{d}$
So, we can say that:
${{B}^{\backslash }}E={{B}^{\backslash }}L$${{A}^{\backslash }}E={{A}^{\backslash }}H$
Now we can write that:
$\begin{align}
  & M=2(x+y); \\
 & h=x+y; \\
 & H=2h \\
\end{align}$$\tan {{i}_{2}}=\dfrac{{{B}^{\backslash }}E}{d}$
And we can say that $\tan {{i}_{2}}=\dfrac{{{B}^{\backslash }}L}{d}$
So, we can say that:
${{B}^{\backslash }}E={{B}^{\backslash }}L$
Now we can say that:
$\begin{align}
  & M=2(x+y); \\
 & h=x+y; \\
 & H=2h \\
\end{align}$
The minimum height of the mirror to see the full image is half of the height of men.

So, the correct answer is option B.

Note: Focal length can also change the perspective and scale of your images. A lens with a shorter focal length “expands” perspective, giving the appearance of more space between the elements in your photo. Meanwhile, telephoto lenses tend to stack elements in the frame together to “compress” perspective. One of the most important aspects, when you buy a lens, is the focal length. This lets you know how close you need to be in relation to the subject you are capturing. A longer focal length is necessary for objects further away. A smaller focal length captures more of the scene in front of us.