Question

The rear side of a truck is open and a box of 40 kg is placed 5 m away from the rear end. The coefficient of friction of the box with the surface of the truck is 0.15. The truck starts from the rest with $2m/{s^2} $acceleration. Calculate the distance covered by the truck when the box falls off
(A) 20m
(B) 30m
(C) 40m
(D) 50m

Answer 1

Hint To answer this question we have to use the second equation of motion to calculate the time t. This should be calculated considering the mass of the box and the acceleration of the truck. Once we obtain the time we need to find the distance from the expression of motion. This will give us the answer to the required question. We should know that linear momentum is defined as the product of a system's mass multiplied by its velocity. In symbols, linear momentum is expressed as . Momentum is directly proportional to the object's mass and also its velocity. Thus, the greater an object's mass or the greater its velocity, the greater its momentum. Note that the linear moment is a vector quantity and is conserved in any direction. In the center-of-mass system, the total momentum is always zero, before and after the interaction, in any direction. Angular momentum is inertia of rotation motion. Linear momentum is inertia of translation motion. The big difference is that the type of motion which is related to each momentum is different. It is important to consider the place where the force related to rotation applies, which is appears as 'r' in the formula

Complete step by step answer
It given that the rear side of the truck is open and a box which is 40 kg of mass is placed 5 m away from the open end as shown in the figure:

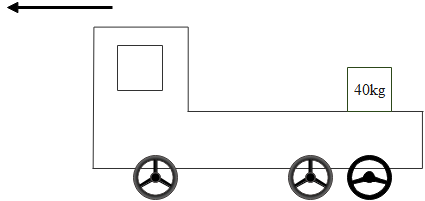
The coefficient of friction between the box and the surface below is given as 0.15. On a straight road, the truck starts from the rest and accelerates with $2m/{s^2} $.
Now let us see the diagrams of the truck and the box individually as given below:


Now we have to find the distance travelled by the truck by the time the box falls from the truck.
So the mass is 40 kg.
The initial velocity or u is 0.
The acceleration is a which is $2m/{s^2} $.
The distance is given as S which is 5 m.
So the force is given by F = ma
Now we have to put the values to get the expression as:
 $F = 40 \times 2 = 80N $
This is because of the acceleration of trucks.
So we can write the $f = \mu mg $
So substituting the values in the above expression we get:
 $ \Rightarrow f = 0.15 \times 40 \times 10 = 60N $
So the net force acting on the block will be given as:
 ${{\text{F}}_{{\text{net}}}}{\text{ = (80 - 60) N = 20N backward}} $
Now the backward acceleration produced is:
 ${a_{back}} = \dfrac{{{F_{net}}}}{m} = \dfrac{{20}}{{40}} = 0.5m/{s^2} $
Using the second equation of the motion, time t can be calculated as:
 $
  {S} = ut + \dfrac{1}{2}{a_{back}}{t^2} \\
   \Rightarrow S = 0 + \dfrac{1}{2} \times 0.5 \times {t^2} \\
   \Rightarrow t = \sqrt {20S} \\
  $
Now we have to apply the speed and distance formula:
The distance S travelled by the truck in ${(\sqrt {20} )^2} $
Now applying the distance equation to get:
 $
   \Rightarrow S = ut + \dfrac{1}{2}a{t^2} \\
   \Rightarrow S = 0 + \dfrac{1}{2} \times 2 \times {(\sqrt {20} )^2} \\
   \Rightarrow S = 20m \\
  $

So we can say that the distance covered by the truck when the box falls off is 20 m. Hence the correct option A.

Note We should know that the second equation of the motion that we have used in the answer gives us a displacement of a body under the influence of a constant acceleration. There are in total three equations of motion. The equations of motion help us to develop a relationship between the velocity, time, acceleration and displacement. We know that momentum is a physics term that refers to the quantity of motion that an object has. A sports team that is on the move has the momentum. If an object is in motion (on the move) then it has momentum. One example is the use of air bags in automobiles. Air bags are used in automobiles because they are able to minimize the effect of the force on an object involved in a collision. Air bags accomplish this by extending the time required to stop the momentum of the driver and passenger. Momentum is mass in motion, and any moving object can have momentum. An object's change in momentum is equal to its impulse. Impulse is a quantity of force times the time interval. Impulse is not equal to momentum itself; rather, it's the increase or decrease of an object's momentum. Based on this concept we have to solve this question.