Question

The ratio of equivalent resistance across A and B when switch is open to that when switch is closed is:


(A) $\dfrac{3}{8}$
(B) $\dfrac{5}{8}$
(C) $\dfrac{7}{8}$
(D) $\dfrac{9}{8}$

Answer 1

Hint: We know that resistance is a measure of the opposition to current flow in an electrical circuit. Resistance is measured in ohms, symbolized by the Greek letter omega. Resistance is an electrical quantity that measures how the device or material reduces the electric current flow through it. The resistance is measured in units of ohms (Ω). If we make an analogy to water flow in pipes, the resistance is bigger when the pipe is thinner, so the water flow is decreased. Based on this concept we have to solve this question.

Complete step-by-step answer:
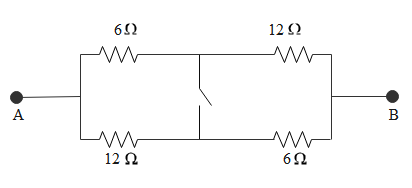
When the switch is open, $6\Omega $and $12\Omega $are connected in series. $12\Omega $ and $6\Omega $ are also connected in series and both are in parallel connection.
So, ${{R}_{AB}}=\left( 6+12 \right)||\left( 12+6 \right)$
$\Rightarrow {{R}_{AB}}=18||18=9\Omega $
When the switch is closed, $6\Omega $and $12\Omega $are connected in parallel. $12\Omega $ and $6\Omega $ are also connected in parallel and both are in series connection.
So, ${{{R}'}_{AB}}=\left[ 6||12 \right]+\left[ 12||6 \right]$
Or, $6||12$=$\dfrac{6\times 12}{6+12}=4\Omega $
Or, ${{{R}'}_{AB}}=4+4=8\Omega $
Ratio $\dfrac{{{{{R}'}}_{AB}}}{{{{{R}'}}_{AB}}}=\dfrac{9}{8}$

Hence, the correct answer is Option D.

Note: We know that components connected in parallel are connected along multiple paths so that the current can split up. The same voltage is applied to each component. A circuit composed solely of components connected in series is known as a series circuit; likewise, one connected completely in parallel is known as a parallel circuit. The parallel circuit is the standard electrical circuit found in most homes and devices. Because it provides more than one way for a current to flow through to a device, it creates a much more stable and efficient power system than would otherwise be possible.
It should be known to us that components connected in series are connected along a single conductive path, so the same current flows through all of the components but voltage is dropped (lost) across each of the resistances. In a series circuit, the sum of the voltages consumed by each individual resistance is equal to the source voltage.