
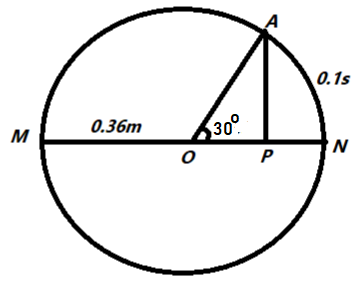
The point A moves with a uniform speed along the circumference of a circle of radius $0.36m$ and covers ${30^\circ }$ in $0.1s$ . The perpendicular projection ‘P’ from ‘A’ on the diameter MN represents the simple harmonic motion of ‘P’. The restoring force per unit mass when P touches M will be:
A. $100N$
B. $50N$
C. $9.87N$
D. $0.49N$
Answer
218.1k+ views
Hint: Restoring force acts to return a body to its equilibrium position and this force is always directed back toward the equilibrium position of the system and depends only on the position of the particle. In this problem first we need to calculate the time period for completing the whole circle and from that angular frequency can be calculated. Finally we can use the formula Restoring Force(F) $ = m{\omega ^2}A$ to get the required answer.
Formula Used:
$\omega = \frac{{2\pi }}{T}$
Restoring Force(F) $ = m{\omega ^2}A$
Here $\omega =$Angular frequency
$T=$Time period for completing the whole circle
$m=$mass of the particle
$A=$ Radius of the circle
Complete step by step solution:
Here in this question given that,
The radius of the circle = $0.36\,m$
Cover angle = ${30^\circ }$
Time taken in covering the angle = $0.1s$
Here from this data we get that,
The point A covers ${30^\circ }$ in $0.1s$
Which means that, we also say that,
$\dfrac{\pi }{6} \to 0.1\sec .$
Similarly, as for \[1\] and $2\pi $
$1 \to \dfrac{{0.1}}{{\dfrac{\pi }{6}}}$
And for $2\pi $
$2\pi = 0.1 \times 6 \times \dfrac{{2\pi }}{\pi }$
By doing further solution we get,
$T = 1.2\sec .$
And we also know that,
$\omega = \dfrac{{2\pi }}{T}$
By putting the value of T in above equation we get,
$\omega = \dfrac{{2\pi }}{{1.2}}$
We also the formula of Restoring force is,
Restoring Force(F) $ = m{\omega ^2}A$
For unit mass the Restoring force will be
$\dfrac{F}{m} = {\omega ^2}A$
By putting all the values in above equation,
$\dfrac{F}{m} = {(\dfrac{{2\pi }}{{1.2}})^2} \times 0.36$
By further solution, we get
$\dfrac{F}{m} \simeq 9.87\,N$
From this we get the answer is $ \simeq 9.87\,N$.
Hence, the correct option is C.
Note: As this is a formula based question so you have to know all the formulas which are used in this type of question. For talking about this question, fractional calculation is very important to do the solution correctly as well as the equation putting system also be clear to all for these types of questions.
Formula Used:
$\omega = \frac{{2\pi }}{T}$
Restoring Force(F) $ = m{\omega ^2}A$
Here $\omega =$Angular frequency
$T=$Time period for completing the whole circle
$m=$mass of the particle
$A=$ Radius of the circle
Complete step by step solution:
Here in this question given that,
The radius of the circle = $0.36\,m$
Cover angle = ${30^\circ }$
Time taken in covering the angle = $0.1s$
Here from this data we get that,
The point A covers ${30^\circ }$ in $0.1s$
Which means that, we also say that,
$\dfrac{\pi }{6} \to 0.1\sec .$
Similarly, as for \[1\] and $2\pi $
$1 \to \dfrac{{0.1}}{{\dfrac{\pi }{6}}}$
And for $2\pi $
$2\pi = 0.1 \times 6 \times \dfrac{{2\pi }}{\pi }$
By doing further solution we get,
$T = 1.2\sec .$
And we also know that,
$\omega = \dfrac{{2\pi }}{T}$
By putting the value of T in above equation we get,
$\omega = \dfrac{{2\pi }}{{1.2}}$
We also the formula of Restoring force is,
Restoring Force(F) $ = m{\omega ^2}A$
For unit mass the Restoring force will be
$\dfrac{F}{m} = {\omega ^2}A$
By putting all the values in above equation,
$\dfrac{F}{m} = {(\dfrac{{2\pi }}{{1.2}})^2} \times 0.36$
By further solution, we get
$\dfrac{F}{m} \simeq 9.87\,N$
From this we get the answer is $ \simeq 9.87\,N$.
Hence, the correct option is C.
Note: As this is a formula based question so you have to know all the formulas which are used in this type of question. For talking about this question, fractional calculation is very important to do the solution correctly as well as the equation putting system also be clear to all for these types of questions.
Recently Updated Pages
Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Algebra Made Easy: Step-by-Step Guide for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

How to Convert a Galvanometer into an Ammeter or Voltmeter




