Question

The pipe shows the volume flow rate of an ideal liquid at a certain time and its direction. What is the value of \[Q\] in \[\dfrac{{{m^3}}}{s}\] ? ( Assume steady state and equal area of cross- section at each point).


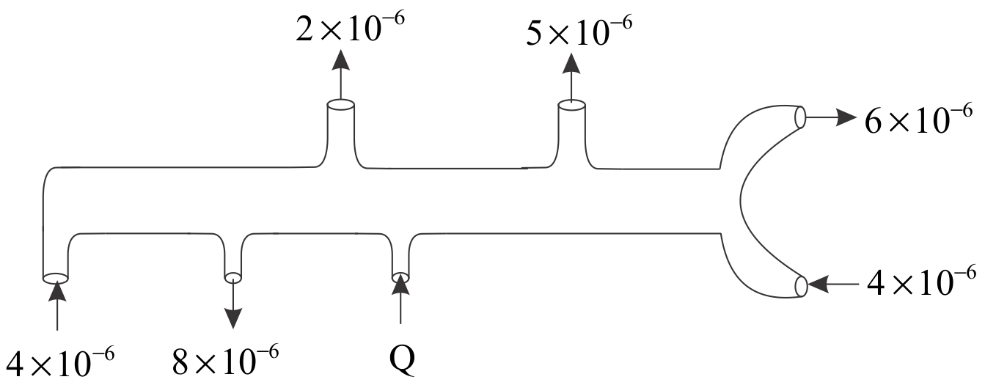
(A) $10 \times {10^{ - 6}}$
(B) $11 \times {10^{ - 6}}$
(C) $13 \times {10^{ - 6}}$
(D) $18 \times {10^{ - 6}}$

Answer 1

Hint: Apply the equation of continuity at all sections . The volume flowing inside the pipe will be equal to the volume flowing outside the pipe . All other values ( at each opening ) are given and this is how it can be calculated .

Complete step by step solution: The above problem will be solved by applying a continuity equation. The equation of continuity is based on conservation of mass . It states that the volume entering the pipe will be equal to the volume exiting the pipe ( if there aren’t any frictional losses) .
          

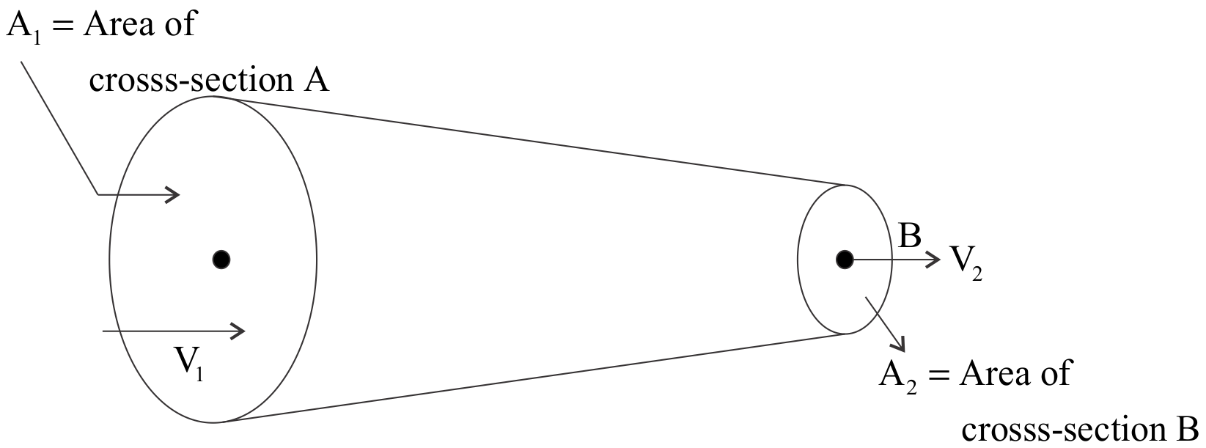
 Suppose we have two sections A and B as shown in the diagram .
${V_1},{V_2}$ are the velocities of each section A and B respectively .
${A_1},{A_2}$ are the corresponding areas of cross- sections .
So according to equation of continuity:
  ${A_1}{V_1} = {A_2}{V_2}$ ……..(i)
The flow rate of liquid is expressed in terms of area and velocity. So eq(i) can be written as :
${Q_1} = {Q_2}$
In the above question, flow rate through each cross- section is given .
Flow rate incoming= flow rate outgoing
We have:
$
  {Q_{in}} = {Q_{out}} \\
  (4 \times {10^{ - 6}}) + (4 \times {10^{ - 6}}) + Q = (2 \times {10^{ - 6}}) + (5 \times {10^{ - 6}}) + (8 \times {10^{ - 6}}) + (6 \times {10^{ - 6}}) \\
  Q = 13 \times {10^{ - 6}} \\
 $

We have got the answer . The correct option is C.

Note: We need to keep in mind that in this derivation we have neglected the loss due to friction . If friction were to be present there will be slight loss in the volume of the liquid .