
The maximum value of \[Z{\text{ = }}4x + 2y\] subject to constraints \[2x + 3y \leqslant 18\] , \[x + y \geqslant 10\] and \[x,y \geqslant 0\] is
(A) \[20\]
(B) \[36\]
(C) \[40\]
(D) None of these
Answer
217.8k+ views
Hint: On converting the given inequalities into equations we get the points to be plotted on the graph. From the graph, we can obtain a feasible point by determining a common point that satisfies all the inequalities simultaneously.
Complete step by step Solution:
Given,
\[Z = 4x + 2y\] subject to constraints \[2x + 3y \leqslant 18\] and \[x + y \geqslant 10\] where \[x \geqslant 0\] and \[y \geqslant 0\]
Let us consider the inequalities as equalities for some time,
\[2x + 3y = 18\] … \[(1)\]
\[x + y = 10\]… \[(2)\]
From \[(1)\] we get \[x = 0 \Rightarrow y = 6\] and \[y = 0 \Rightarrow x = 9\]
So, the points (0,6) and (9,0) lie on the line given in \[(1)\].
From \[(2)\] we get \[x = 0 \Rightarrow y = 10\] and \[y = 0 \Rightarrow x = 10\]
So, the points (0,10) and (10,0) lie on the line given in \[(2)\].
On plotting these points considering the inequalities, we get the graph in which the shaded part shows the feasible region.
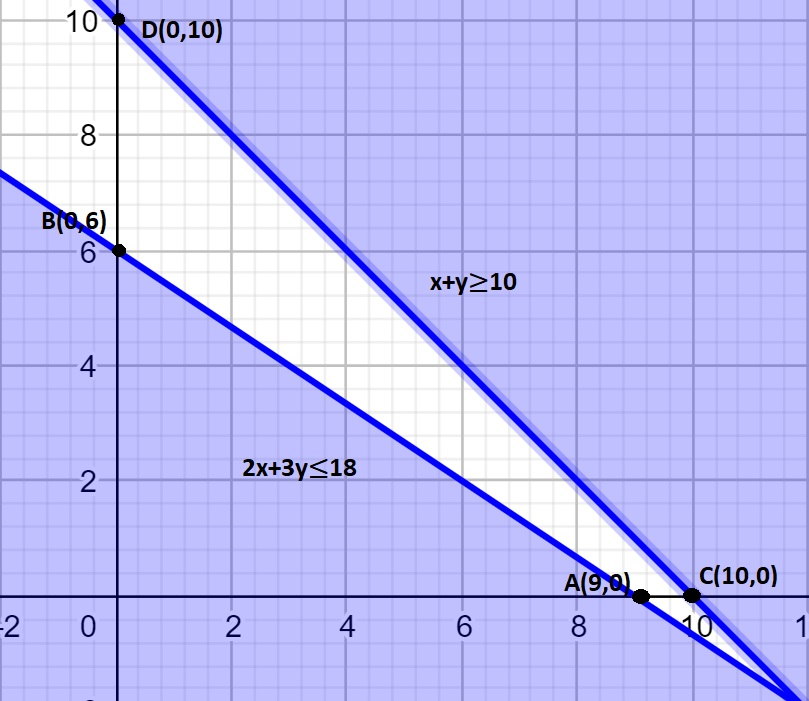
We can clearly see that there is no area in the 1st quadrant where the two inequalities meet.
Hence there is no solution for the LPP with the given constraints and Z cannot be maximized
Hence, the correct option is (D).
Note: The solutions of the LPP are obtained from the point where the inequalities meet. If there is no point in satisfying all the inequations simultaneously then there is no feasible point and the solution is said to be infeasible.
Complete step by step Solution:
Given,
\[Z = 4x + 2y\] subject to constraints \[2x + 3y \leqslant 18\] and \[x + y \geqslant 10\] where \[x \geqslant 0\] and \[y \geqslant 0\]
Let us consider the inequalities as equalities for some time,
\[2x + 3y = 18\] … \[(1)\]
\[x + y = 10\]… \[(2)\]
From \[(1)\] we get \[x = 0 \Rightarrow y = 6\] and \[y = 0 \Rightarrow x = 9\]
So, the points (0,6) and (9,0) lie on the line given in \[(1)\].
From \[(2)\] we get \[x = 0 \Rightarrow y = 10\] and \[y = 0 \Rightarrow x = 10\]
So, the points (0,10) and (10,0) lie on the line given in \[(2)\].
On plotting these points considering the inequalities, we get the graph in which the shaded part shows the feasible region.

We can clearly see that there is no area in the 1st quadrant where the two inequalities meet.
Hence there is no solution for the LPP with the given constraints and Z cannot be maximized
Hence, the correct option is (D).
Note: The solutions of the LPP are obtained from the point where the inequalities meet. If there is no point in satisfying all the inequations simultaneously then there is no feasible point and the solution is said to be infeasible.
Recently Updated Pages
Arithmetic, Geometric & Harmonic Progressions Explained

Cartesian Form of Vector Explained: Formula, Examples & Uses

Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Trending doubts
Understanding Collisions: Types and Examples for Students

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Elastic Collisions in Two Dimensions

Understanding Newton’s Laws of Motion

JEE Main 2026 Syllabus Updated for Physics, Chemistry and Mathematics

Other Pages
NCERT Solutions For Class 11 Maths Chapter 11 Introduction To Three Dimensional Geometry - 2025-26

Inertial and Non-Inertial Frame of Reference Explained

Clemmensen and Wolff Kishner Reductions Explained for JEE & NEET

JEE Main 2023 January 29th Shift 2 Physics Question Paper with Answer Keys and Solutions

Devuthani Ekadashi 2025: Correct Date, Shubh Muhurat, Parana Time & Puja Vidhi

Quadratic Equation Questions with Solutions & PDF Practice Sets




