Question

The maximum refractive index of a prism which permits passage of the light through it when the refracting angle of the prism is 90°, is:
(A) $\dfrac{{\text{1}}}{{\sqrt {\text{2}} }}$
(B) $\sqrt 2 $
(C) $\sqrt {\dfrac{3}{2}} $
(D) $\dfrac{3}{2}$

Answer 1

Hint: Firstly, use the formula for refractive index $\mu = \dfrac{1}{{\sin \left( {{\theta _C}} \right)}}$ and critical angle ${\theta _C} = 90 - r$ to find out sin(r) in terms of refractive index, $\mu$. Secondly, use the other formula for refractive index $\mu = \dfrac{{\sin i}}{{\sin r}}$ to find out sin(i) in terms of refractive index, $\mu $.
Lastly, use the inequality sin(i) ≤ 1, to find out the value of maximum refractive index, $\mu $.

Complete step by step solution


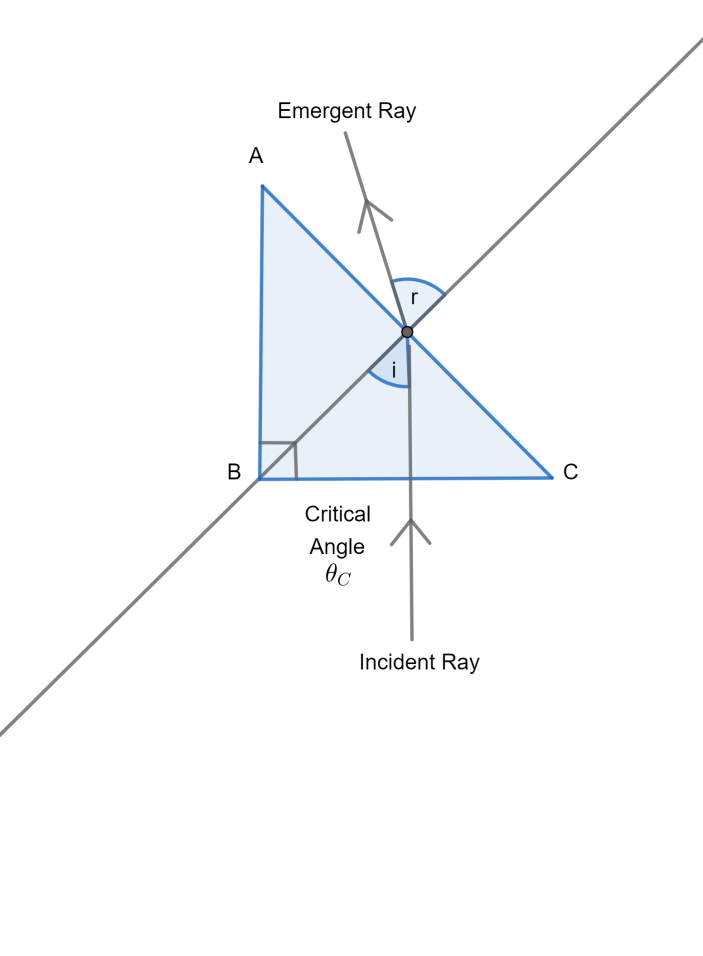
Let the angle of refraction be r and the critical angle for the prism be ${\theta _C}$. Now using the formula for refractive index in terms of the critical angle, ${\theta _C}$:
$\mu = \dfrac{1}{{\sin \left( {{\theta _C}} \right)}}$
Putting ${\theta _C}$= 90 – r in the above equation,
$ \Rightarrow \mu = \dfrac{1}{{\sin \left( {90 - r} \right)}}$
We know that $\sin (90 - r) = \cos r$ (from trigonometry). Putting this in the above equation,
$
   \Rightarrow \mu = \dfrac{1}{{\cos r}} \\
   \Rightarrow \cos r = \dfrac{1}{\mu } \\
 $
Putting the value of cos(r) from the above equation in the general trigonometry relation:
$\sin r = \sqrt {1 - {{\cos }^2}r} $ gives us,
\[
   \Rightarrow \sin r = \sqrt {1 - {{\left( {\dfrac{1}{\mu }} \right)}^2}} \\
   \Rightarrow \sin r = \sqrt {\left( {\dfrac{{{\mu ^2} - 1}}{{{\mu ^2}}}} \right)} \\
   \Rightarrow \sin r = \dfrac{{\sqrt {{\mu ^2} - 1} }}{\mu } \\
 \]
Now, another formula for the refractive index is, $\mu = \dfrac{{\sin i}}{{\sin r}}$ where ‘i' is the angle of incidence.
$ \Rightarrow \sin i = \mu \times \sin r$
Now putting our value of sin(r) in the above equation,
\[
   \Rightarrow \sin i = \mu \times \dfrac{{\sqrt {{\mu ^2} - 1} }}{\mu } \\
   \Rightarrow \sin i = \sqrt {{\mu ^2} - 1} \\
 \]
and also, $\sin i < 1$.
$
   \Rightarrow \sqrt {{\mu ^2} - 1} \leqslant 1 \\
   \Rightarrow {\mu ^2} - 1 \leqslant 1 \\
   \Rightarrow {\mu ^2} \leqslant 2 \\
   \Rightarrow \mu \leqslant \sqrt 2 \\
 $
Therefore, the maximum value of the refractive index will be equal to $\sqrt 2 $ .

Hence, option (B) is correct.

Note: We are given the refracting angle of the prism to be 90° in the question. So, alternatively as a shortcut method, we can just put this in the other formula of refractive index, $\mu = \dfrac{{\sin (A + \delta \min )}}{{\sin \left( {\dfrac{A}{2}} \right)}}$.
Where, A will be 90° and $\delta \min $ will be zero.
$
   \Rightarrow \mu = \dfrac{{\sin (90)}}{{\sin \left( {45} \right)}} \\
   \Rightarrow \mu = \dfrac{1}{{\dfrac{1}{{\sqrt 2 }}}} \\
   \Rightarrow \mu = \sqrt 2 \\
 $