Question

The magnification for a mirror is -3. How are u and v related?

Answer 1

Hint: Before we understand the concept of magnification in a mirror, it is important to understand the magnification is only possible in curved mirrors. In plane mirrors, the magnification is always 1 which means that the image is not enlarged or diminished in a plane mirror and always has the same size of the object. Hence, we have to consider curved mirrors only.

Complete step by step answer:
Magnification of the image is defined as the ratio of height of the image produced by the curved mirror to the ratio of height of the object.
Let us consider an object AB of height ${h_0}$ and distance -u from the pole P placed between centre of curvature C and focus F in front of a concave mirror as shown:

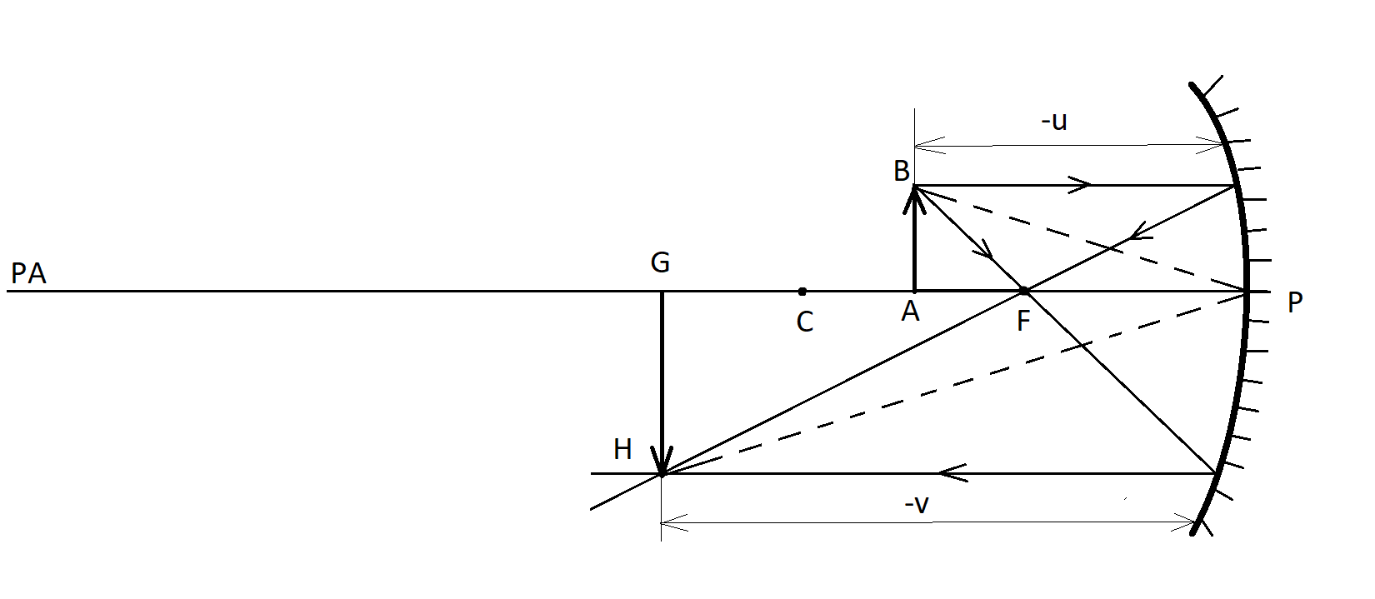
There are two rays emerging from the object.
i) First ray, parallel to the principal axis PA, after reflection, passes through focus.
ii) Second ray, passing through focus, after reflection, passes parallel to the principal axis.
These two rays meet beyond the centre of curvature C, to form the image GH of height ${h_i}$ at distance of -v from the pole.
Consider the triangles ABP and GHP.
$\Rightarrow \angle PAB = \angle PGH = {90^ \circ }$
By the law of reflection that incident angle equal to reflected angle, we have –
$\Rightarrow \angle APB = \angle GPH$
Hence, we can prove that the triangles ABP and GHP are similar.
By rule of similarity, we can say that –
$\Rightarrow \dfrac{{GH}}{{AB}} = \dfrac{{\left( { - v} \right)}}{{\left( { - u} \right)}}$
$ \Rightarrow \dfrac{{GH}}{{AB}} = \dfrac{v}{u}$
Given that $AB = {h_0}$ and $GH = - {h_i}$ (the negative sign is because the height of image is measured downwards direction)
Magnification is equal to the ratio of height of image of height of object.
$\Rightarrow m = \dfrac{{ - {h_i}}}{{{h_0}}}$
Substituting,
$\Rightarrow m = - \dfrac{v}{u}$
Therefore, magnification is defined as the ratio of v to u with a minus sign.

Note: The formula for the magnification in a lens is the same as that of a mirror, but only in the magnitude. The magnification formula for lenses has a positive sign while the magnification formula for a mirror has a negative sign.
Magnification for lens –
$m = \dfrac{v}{u}$
The students must understand the clear distinction between the two so that there is no confusion between the two formulae.