Question

The \[{{\left[ Fe{{\left( CN \right)}_{6}} \right]}^{3-}}\]complex ion:
(A) Exhibits planar geometry
(B) Is diamagnetic
(C) Should be very stable
(D) has 2 unpaired electrons.

Answer 1

Hint: The\[C{{N}^{-}}\]is a strong field ligand. \[{{\left[ Fe{{\left( CN \right)}_{6}} \right]}^{3-}}\]will form an inner orbital complex. Finding the oxidation state of iron will help in determining its hybridization.

Complete step by step solution:
We have been given \[{{\left[ Fe{{\left( CN \right)}_{6}} \right]}^{3-}}\]as our coordination complex. Now first let us find out the oxidation number of iron. As you already know, the cyanide ion has an oxidation number of “$-1$”; taking iron atom’s oxidation state as “x” we form the following equation:
\[\begin{align}
& x+6(-1)=-3 \\
& \Rightarrow x=+3 \\
\end{align}\]
So iron can be seen as- $F{{e}^{3+}}$ . The atomic number of iron is $26$; its electronic configuration becomes: $1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{6}}$. The arrangement of electrons in its orbital is as follows:

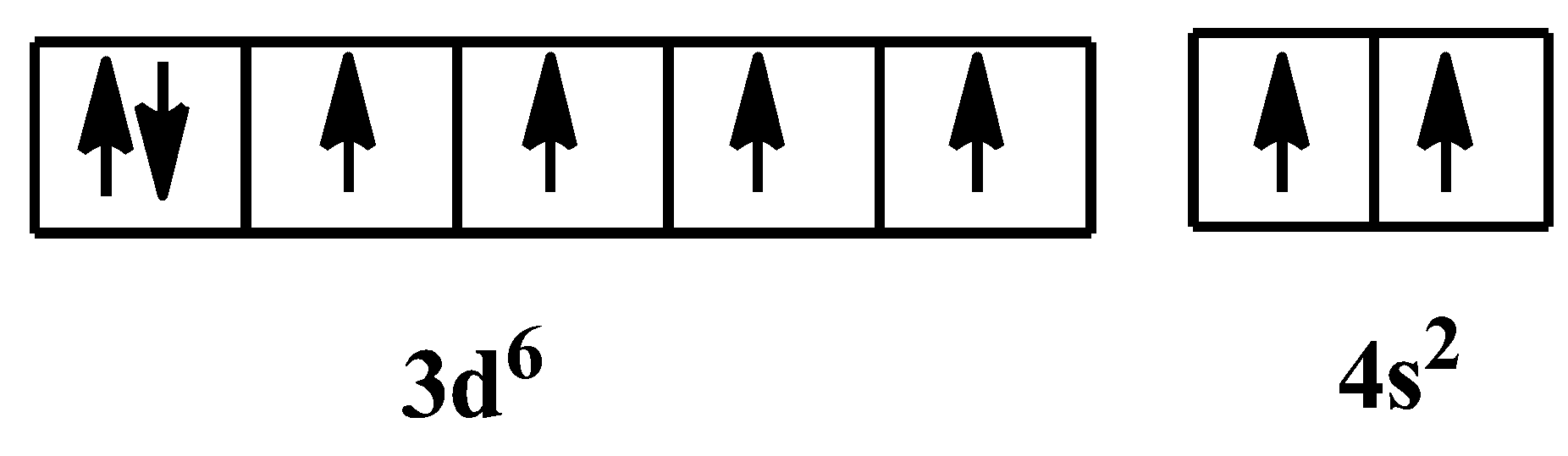
In $F{{e}^{3+}}$ state, its electronic configuration would be:

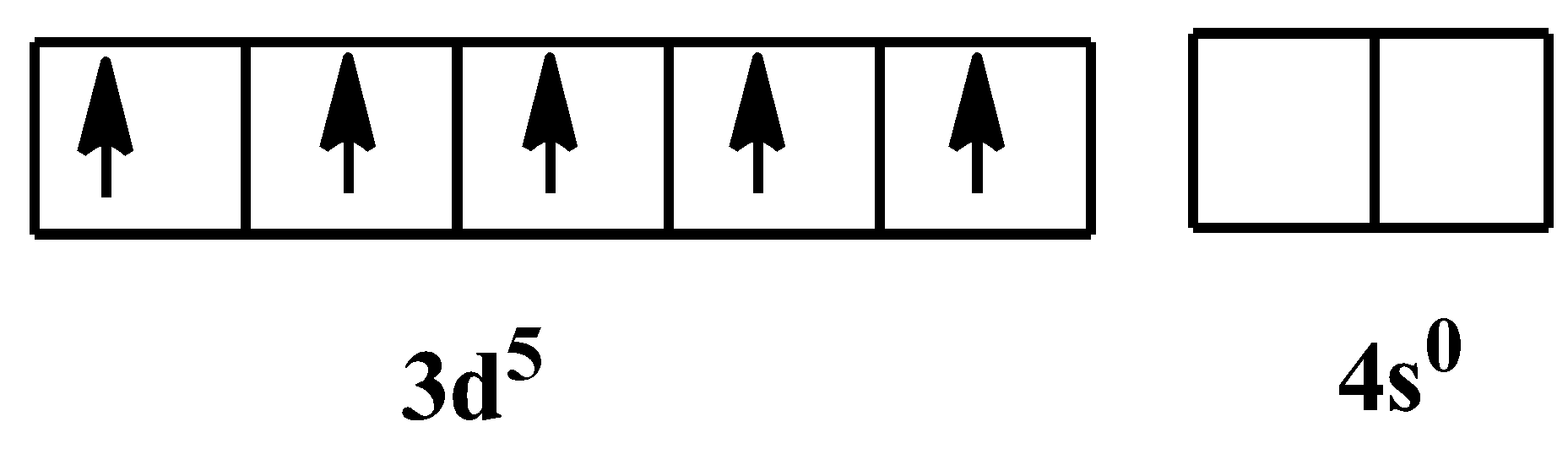
As it is mentioned already in the hint, that cyanide is a strong field ligand, which means it will always form low spin complexes. As there are six of them, so the hybridization would be ${{d}^{2}}s{{p}^{3}}$, which is for octahedral geometry. The orbital configuration in the presence of the ligand would be-

So, the orbital configuration when the ligands would have donated their electrons is:

As you can see, there is one unpaired electron. This makes the coordinate complex paramagnetic in nature. From all the options, only option C is correct. Indeed, the compound is very stable.

Note:
Sometimes, these strong field ligands form low spin complexes. Although these occurrences are very rare, students are still advised to memorize some of these exceptions. Cyanide and CO are some of these.