Question

what will be the force constant of the spring system shown in the figure,

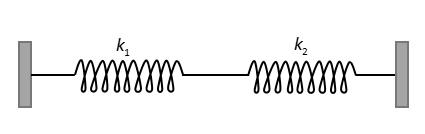
Fig: The spring mass system
A. \[{k_1} + {k_2}\]
B. \[\dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}}\]
C. \[{k_1} - {k_2}\]
D. \[\dfrac{{{k_1}{k_2}}}{{{k_1} - {k_2}}}\]

Answer 1

Hint: The equivalent spring constant of the system of springs is the single value of the spring constant which will be having same effect as the combination of the springs. So, the combination of the springs can be replaced by a single spring which is having spring constant equivalent to the combination of those springs.

Formula used:
\[{K_{eq}} = {k_1} + {k_2} + {k_3} + \ldots + {k_n}\], the formula for the equivalent spring constants when n springs are connected in parallel with spring constants \[{k_1},{k_2},{k_3} \ldots \ldots \]
\[\dfrac{1}{{{K_{eq}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} + \dfrac{1}{{{k_3}}} + \ldots + \dfrac{1}{{{k_n}}}\], the formula for the equivalent spring constants when n springs are connected in series with spring constants \[{k_1},{k_2},{k_3} \ldots \ldots \]

Complete step by step solution:

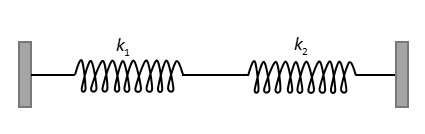
Fig: The spring mass system
When we take a point at the junction of the two given springs and displace it in either direction, left or right; we observe that the displacement in both the springs are same as the displacement made at the joint of the springs.

Hence, the springs with spring constants \[{k_1}\] and \[{k_2}\]are connected in parallel with each other. So the equivalent of these two springs will be calculated using formula for the equivalent spring constant when the springs are connected in parallel,

Let the equivalent spring constant of the two springs with spring constants\[{k_1}\]and \[{k_2}\]is \[{k_{eq}}\],

Using the formula, we get
\[{k_{eq}} = {k_1} + {k_2}\]

So, the equivalent spring constant of the given spring system is \[{k_1} + {k_2}\]

Therefore, the correct option is (C).

Note: We should be careful while identifying the type of combinations the spring has. The best way to decide whether the combination is series or parallel, we displaces the joint. If the combination is in parallel then the change in length of the springs will be same otherwise the combination will be series.