Question

The following graphs show the horizontal position versus the vertical position for different projectiles based on the colours of the projectiles (air resistance negligible). All projectiles are launched from the same horizontal surface, under the same conditions. What is the rank for the projectile for the time they spend in the air (greatest first)?

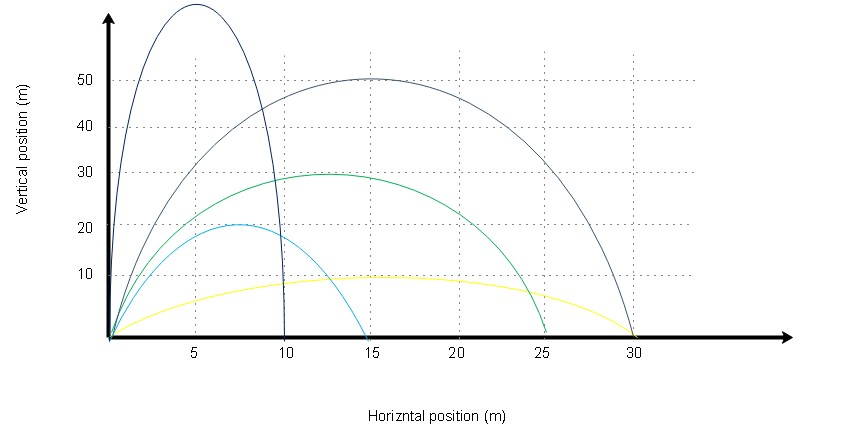
A) Red and yellow tie, green, blue, purple
B) Red, purple and green tie, blue and yellow tie
C) Red, yellow, green, blue, purple
D) Purple, red, green, blue, yellow
E) Not enough information is given to answer this question

Answer 1

Hint: The time spent by the projectile in the air depends on the initial velocity of the object, the angle of projection, and the gravitational acceleration. We will find the dependence of the time of flight on only the maximum height achieved by the projectile.
Formula used: In this solution, we will use the following formula:
Flight time of projectile: $T = \dfrac{{2u\sin \theta }}{g}$ where $u$ is the launch velocity, $\theta $ is the launch angle, and $g$ is the gravitational acceleration
Maximum height of a projectile: $H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$

Complete step by step answer:
We want to find the order of the time of flight of different projectiles given in the image. The flight time of a projectile is measured as
$T = \dfrac{{2u\sin \theta }}{g}$
But we can see in this formula that all the projectiles will have a different initial velocity and a different angle of projection and we don’t have direct information of the initial velocity of the projectile. But we do have the information on the range of the projectile and the maximum height achieved by the projectile that can be inferred from the image.
Then using the formula for the maximum height of a projectile, we can write
$H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
This can be rearranged to write
${u^2}{\sin ^2}\theta = 2gH$
Taking the square root on both sides, we get
$u\sin \theta = \sqrt {2gH} $
Substituting this value in the formula for the time of flight formula, we get
$T = \dfrac{{2\sqrt {2gH} }}{g}$
We can see in this formula that the only variable that will be different for different projectiles will be the maximum height of the projectile. Hence as
$T \propto \sqrt H $
The higher the maximum height of the projectile, the higher the time of flight and vice versa. So, from the graph, we can see that the order of time of flight will be
-Purple, red, green, blue, yellow

Hence the correct choice is option (D).

Note: While option (D) does not have all the colours, it is the only option containing the correct order of the time of flight of the projectile. We must find such a dependence of the time of flight that it only depends on one variable and all the other variables in the formula remain constant for all the projectiles to directly compare the time of flight of different projectiles based on the one variable which in this case is the maximum height of the projectile.