
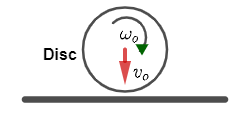
The figure shown is just before collision, the velocity of the centre of uniform disc is ${v_0}$ vertically downward & ${\omega _0}$ is the angular velocity as shown. If it is found that collision is elastic and after collision disc stops rotating then if coefficient of friction is \[\left( {\dfrac{1}{P}} \right)\] then the value of P is? If ${v_0} = R{\omega _0}$ . (R is radius of disc)
Answer
218.4k+ views
Hint:The friction coefficient is the ratio of the normal force pressing two surfaces together to the frictional force preventing motion between them. Typically, it is represented by the Greek letter mu ( $\mu $ ). In terms of maths, it is equal to $\mu = \dfrac{F}{N}$ , where F stands for frictional force and N for normal force.
Formula Used:
Velocity of uniform disc, ${v_0} = R{\omega _0}$
Linear Momentum, $p = mv$
Angular Momentum, $L = mvr$
Complete step by step solution:
As we know that, because we have to find the velocity of the disc, firstly we calculate the change in linear momentum. Substitute the mass, beginning, and end velocities into the equation above to get the change in momentum,
Change in Momentum $ = 2m{v_0}$
As from above equation, we get the value of change in momentum, by which we can easily find the value of Angular Impulse,
Angular impulse $ = R \times \text{Linear impulse} \times \mu (friction)$
Angular impulse $ = 2m{v_0}R \times \mu $
As in the above equation, $2m{v_0}R$ is the change in angular momentum as we can also calculate it with the help of his formula which is given above.
Now, we know that,
$2m{v_0}R\mu = I{\omega _0}$
As according to the question, by making changes in the above equation as we know that,
$\dfrac{{2m{v_0}R}}{P} = \dfrac{{m{R^2}}}{2}{\omega _0}$
As, according to the question, we need the value of P so,
$P = \dfrac{{4{v_0}}}{{R{\omega _0}}}$
As we know that, ${v_0} = R{\omega _0}$ out form this making suitable changes in above equation we get,
$P = 4$
Therefore, the correct answer for the coefficient of friction is $P = 4$.
Note: An elastic collision is one in which the system does not experience a net loss of kinetic energy as a result of the collision. In elastic collisions, momentum and kinetic energy are both conserved. There is no net conversion of kinetic energy into other forms, such as heat, noise, or potential energy, in an ideal, fully elastic collision.
Formula Used:
Velocity of uniform disc, ${v_0} = R{\omega _0}$
Linear Momentum, $p = mv$
Angular Momentum, $L = mvr$
Complete step by step solution:
As we know that, because we have to find the velocity of the disc, firstly we calculate the change in linear momentum. Substitute the mass, beginning, and end velocities into the equation above to get the change in momentum,
Change in Momentum $ = 2m{v_0}$
As from above equation, we get the value of change in momentum, by which we can easily find the value of Angular Impulse,
Angular impulse $ = R \times \text{Linear impulse} \times \mu (friction)$
Angular impulse $ = 2m{v_0}R \times \mu $
As in the above equation, $2m{v_0}R$ is the change in angular momentum as we can also calculate it with the help of his formula which is given above.
Now, we know that,
$2m{v_0}R\mu = I{\omega _0}$
As according to the question, by making changes in the above equation as we know that,
$\dfrac{{2m{v_0}R}}{P} = \dfrac{{m{R^2}}}{2}{\omega _0}$
As, according to the question, we need the value of P so,
$P = \dfrac{{4{v_0}}}{{R{\omega _0}}}$
As we know that, ${v_0} = R{\omega _0}$ out form this making suitable changes in above equation we get,
$P = 4$
Therefore, the correct answer for the coefficient of friction is $P = 4$.
Note: An elastic collision is one in which the system does not experience a net loss of kinetic energy as a result of the collision. In elastic collisions, momentum and kinetic energy are both conserved. There is no net conversion of kinetic energy into other forms, such as heat, noise, or potential energy, in an ideal, fully elastic collision.
Recently Updated Pages
Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Algebra Made Easy: Step-by-Step Guide for Students

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

How to Convert a Galvanometer into an Ammeter or Voltmeter




