Question

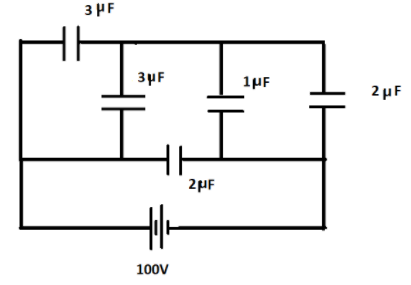
The figure showed a network of five capacitors connected to a $100V$ supply. Calculate the total energy stored in the network.

Answer 1

Hint: In order to solve this question, one should be aware of the concept of calculating the equivalent capacitance of the circuit. After calculating the equivalent capacitance of the circuit, put that capacitance in the formula of energy and the total energy stored in the network will be calculated. As the Potential Difference of the circuit is also given.

Complete step by step answer:
Here, the potential difference across the circuit is given.
That is, $V = 100V$
Now, we have to calculate the capacitance of the circuit.
Here the capacitors of $3\mu F$ and $3\mu F$ are in parallel combination. Hence, their equivalent capacitance would be,
$3\mu F + 3\mu F = 6\mu F$
Also the capacitors of capacitance $1\mu F$ and $2\mu F$ are in parallel combination. Hence, their equivalent capacitance would be,
$1\mu F + 2\mu F = 3\mu F$

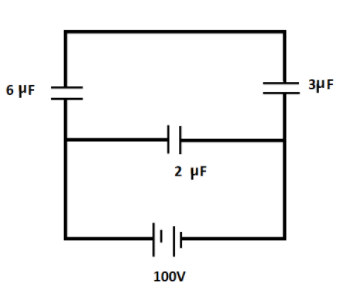
Now in the above circuit we have capacitors of capacitance $6\mu F$ and $3\mu F$ in series combination. Hence, their equivalent capacitance would be,
$\dfrac{1}{{{C'}}} = \dfrac{1}{{6\mu F}} + \dfrac{1}{{3\mu F}}$
On solving, we get
${C'} = 2\mu {F^{}}$
Now we have these two capacitors of capacitance $2\mu F$ and $2\mu F$ in parallel combination. Hence, their equivalent resistance would be,
$C = 2\mu F + 2\mu F$
Hence we get the total capacitance of the circuit as,
$C = 4\mu F$
Now, the energy stored in the circuit is given by
$E = \dfrac{1}{2}C{V^2}$
Here, $C$ is the capacitance of the circuit.
$V$ is the voltage drop across the circuit.
Here in this question we are given with $V$ and that is,
$V = 100V$
Also, we just have calculated the capacitance as $C = 4\mu F$ .
Putting the values of $V$ and $C$ in the energy equation we have,
$E = \dfrac{1}{2}\left( {4 \times {{10}^{ - 6}}} \right){(100)^2}$
On solving we get,
$E = 2 \times {10^{ - 2}}J$

Hence the total energy stored in the circuit is $E = 2 \times {10^{ - 2}}J$.

Note: It is important to note that in the parallel combination, the equivalent capacitance of the capacitors would be the sum of the individual capacitances. While in series combination the reciprocal of the equivalent capacitance would be equal to the sum of reciprocals of individual capacitance of the capacitors.