Question

The equivalent resistance between X and Y will be


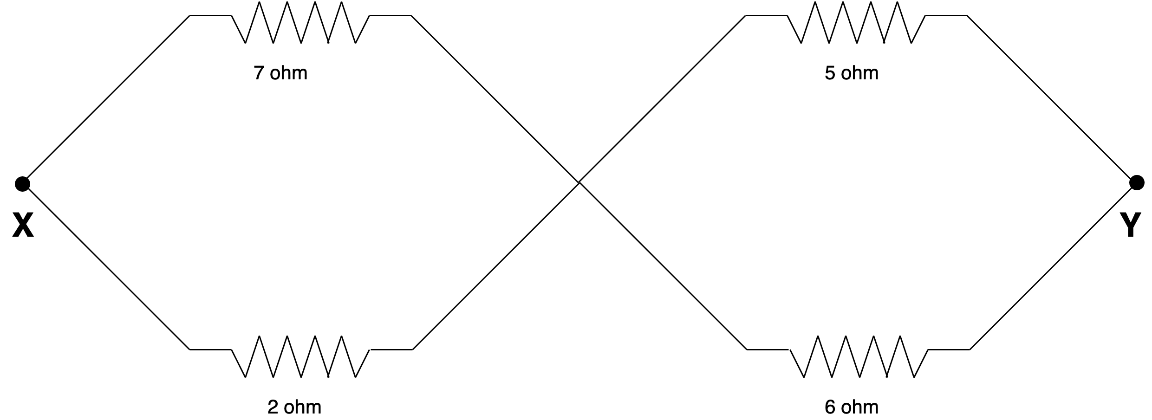
A) 4 ohm
B) 4.5 ohm
C) 2 ohm
D) 20 ohm.

Answer 1

Hint: Resistors are said to be in parallel when their two terminals connect to the same node. On the other hand, resistors are said to be in series when they are connected head-to-tail and there is no other wire branching off from the nodes between components. For example, in the above circuit, the resistors 7 ohm and 2 ohm are connected parallel.

Complete step by step solution:
Step 1: first we will calculate the equivalent resistance $R'$ of the 7ohm and 2 ohm. Express the formula for the equivalent resistance when two resistors are connected parallel.
$\therefore \dfrac{1}{{R'}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ , where $R'$ is the equivalent resistor of the 7 ohm and 2 ohm.
Step 2: Substitute the values for ${R_1}$ and ${R_2}$
$\therefore \dfrac{1}{{R'}} = \dfrac{1}{7} + \dfrac{1}{2}$
$ \Rightarrow \dfrac{1}{{R'}} = \dfrac{9}{{14}}$
Step 3: Take the reciprocal on both sides
\[\therefore R' = \dfrac{{14}}{9}\]
Step 4: Now similarly calculate the equivalent resistance $R''$ of 5 ohm and 6 ohm which is also parallel.
$\therefore \dfrac{1}{{R''}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
Step 5: Substitute the values for ${R_1}$ and ${R_2}$
$\therefore \dfrac{1}{{R''}} = \dfrac{1}{5} + \dfrac{1}{6}$
$ \Rightarrow \dfrac{1}{{R''}} = \dfrac{{11}}{{30}}$
Step 6: Now our circuit will be

Now clearly you can see that there are two resistors in our circuit and both are connected in a series. Express the formula for the equivalent resistance of the two resistors connected in series.
$\therefore {R_{equ}} = {R_1} + {R_2}$
Step 7: Now substitute the values $\dfrac{{14}}{9}$ for ${R_1}$ and $\dfrac{{11}}{{30}}$ for ${R_2}$
$\therefore {R_{equ}} = \dfrac{{14}}{9} + \dfrac{{11}}{{30}}$
$ \Rightarrow {R_{equ}} \simeq 2$ ohm

Hence the correct option is Option C.

Note: While calculating equivalent resistance in a circuit always remember that the resistors connected parallel should be added first. After adding all parallel resistors the entire circuit will become simple where all the remaining resistors will be connected in series. Resistors connected in series are easier to find equivalent resistance.