Question

The equivalent circuit is:

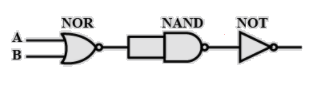
(A) NAND gate
(B) OR gates
(C) AND gates
(D) NOR gates

Answer 1

Hint: From the question we know that the circuit has a NOR gate, NAND gate, and a NOT gate. The input is sent to the NOR gate and the output of that becomes the input for NAND and the output of the NAND gate becomes the input for NOT gate. What exactly happens in each of these gates,
(1) In a NOR gate, the output is the inverse of the sum of A and B. (NOR, $OUTPUT = \overline {A + B} $).
(2) In a NAND gate, the output is the inverse of the multiplication of A and B. (NAND, $OUTPUT = \overline {A.B} $).
(3) in a NOT gate the output is the inverse of the input, the input of a NOT gate is always a single digit. ( NOT,$OUTPUT = \overline A $).

Complete step by step solution:
Taking outputs of all the gates as ${y_1},{y_2},{y_3}$,



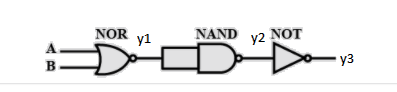
We know that a NOR gate inverses the sum of its inputs , so output at NOR is ${y_1} = \overline {A + B} $
${y_1}$ becomes the input for NAND gate , so $\overline {{y_1}.{y_1}} = {y_2} = \overline {\overline {A + B} .\overline {A + B} } = \overline {\overline {A + B} } + \overline {\overline {A + B} } = A + B$
${y_2}$ become the input for NOT gate , so, ${y_3} = \overline {{y_2}} = \overline {A + B} $
The output for the NOT gate is ${y_3}$ which is the final output and we get the output as the inverse of the sum of A and B which is nothing but the output of NOR gate.
Here, ${y_1},{y_2},{y_3}$ are the outputs of NOR, NAND and NOT gates respectively . The final output is ${y_3}$.

Hence option (D), NOR gate is the correct answer.

Note: Do not get confused with the diagram as OR and AND and NOT the small circle beside each of the gates makes them NOR and NAND gates. It represents the negation of OR and AND. The N represents “negation of” which means the inverse.