Question

The equation $2{{\cos }^{-1}}x+{{\sin }^{-1}}x=\dfrac{11\pi }{6}$ .
(a) No solution.
(b) Only one solution
(c) Two solutions
(d) Three solutions

Answer 1

Hint: Start by using the identity ${{\cos }^{-1}}x+{{\sin }^{-1}}x=\dfrac{\pi }{2}$ and rearrange the equation to get an equation of the form ${{\cos }^{-1}}x=k$ , where k is constant. Now if k lies in the range of ${{\cos }^{-1}}x$ then the equation may have solutions else the equation will never have a solution.

Complete step-by-step answer:
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain.
Now let us draw the graph of $co{{s}^{-1}}x$ .

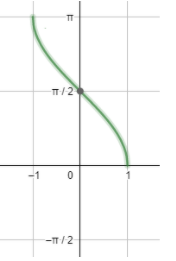
So, looking at the above graphs, we can draw the conclusion that ${{\cos }^{-1}}x$ is defined for all real values of $x\in [-1,1]$ , while its range comes out to be $\left[ 0,\pi \right]$ . The domain of ${{\sin }^{-1}}x$ is same as that of ${{\cos }^{-1}}x$ but its range is $\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$ .
Now moving to the solution to the above question, we will start with the simplification of the expression given in the question.
$2{{\cos }^{-1}}x+{{\sin }^{-1}}x=\dfrac{11\pi }{6}$
We know that ${{\cos }^{-1}}x+{{\sin }^{-1}}x=\dfrac{\pi }{2}$ for all x lying in the domain of ${{\cos }^{-1}}x$ and ${{\sin }^{-1}}x$ .
$co{{s}^{-1}}x+{{\cos }^{-1}}x+{{\sin }^{-1}}x=\dfrac{11\pi }{6}$
$\Rightarrow co{{s}^{-1}}x+\dfrac{\pi }{2}=\dfrac{11\pi }{6}$
$\Rightarrow co{{s}^{-1}}x=\dfrac{11\pi }{6}-\dfrac{\pi }{2}$
$\Rightarrow co{{s}^{-1}}x=\dfrac{11\pi -3\pi }{6}=\dfrac{8\pi }{6}=\dfrac{4\pi }{3}$
Now as $\dfrac{4\pi }{3}$ is greater than $\pi $ , we can say that the equation can never be true as $co{{s}^{-1}}x$ can never be greater than $\pi $ , So, the equation has no solution.
Therefore, the answer to the above question is option (a).

Note: Students generally get confused in the range of different inverse trigonometric functions as they very much look the same but are far different. Also, it is important that you check the domain of each inverse trigonometric term in the equation separately before reporting a value of x that satisfies the equation.