Question

The electronic spectrum of \[{{\rm{[Ti(}}{{\rm{H}}_{\rm{2}}}{\rm{O)]}}^{{\rm{3 + }}}}\] shows a single broad peak with a maximum of \[{\rm{20,300c}}{{\rm{m}}^{{\rm{ - 1}}}}\]. The crystal field stabilisation energy (CFSE) of the complex ion, in kJ/mol, is:
(\[{\rm{1kJmo}}{{\rm{l}}^{{\rm{ - 1}}}}{\rm{ = 83}}{\rm{.7c}}{{\rm{m}}^{{\rm{ - 1}}}}\].)
(1) 83.7
(2) 242.5
(3) 145.5
(4) 97

Answer 1

Hint: The crystal field theory (CFT) is an electrostatic model which supposes that the metal-ligand bond is formed due to electrostatic interactions between the metal ion and the ligand. Ligands are regarded as point charges for anions or point dipoles for neutral molecules.

Formula Used:
Crystal field stabilisation energy, CFSE for \[{{\rm{[Ti(}}{{\rm{H}}_{\rm{2}}}{\rm{O)]}}^{{\rm{3 + }}}}\] = \[\dfrac{{{\rm{ - 2}}}}{{\rm{5}}}{\rm{ \times (magnitude \ of \ crystal \ field \ splitting)}}\].

Complete Step by Step Solution:
The five d-orbitals in an isolated gaseous state have a similar energy, which implies that they are degenerate.
However, when a ligand approaches a central metal atom, the degeneracy of the d orbitals is lost.
It results in the splitting of the d-orbitals.
The structure of splitting relies on the nature of the crystal field.

\[{{\rm{[Ti(}}{{\rm{H}}_{\rm{2}}}{\rm{O)]}}^{{\rm{3 + }}}}\] is an octahedral complex.

In an octahedral coordination entity with six ligands enclosing the metal atom/ion, there will be repulsion between the electrons in d orbitals of the metal and the electrons of the ligands.
This repulsion is extra when the metal d orbital is near the ligand than when it is away from the ligand.

Thus, the \[{{\rm{d}}_{{{\rm{x}}^{\rm{2}}}{\rm{ - }}{{\rm{y}}^{\rm{2}}}}}\] and \[{{\rm{d}}_{{{\rm{z}}^{\rm{2}}}}}\] orbitals that lie towards the axes along the direction of the ligand will suffer more repulsion and will be increased in energy.

The $d_{xy}, \ d_{yz}, \ d_{zx}$ orbitals which lie between the axes will be reduced in energy compared to the average energy in the spherical crystal field.
Therefore, the degeneracy of the d orbitals has been eliminated due to ligand electron-metal electron repulsions in the octahedral complex.
It results in three orbitals of lower energy, \[{{\rm{t}}_{{\rm{2g}}}}\] set, and two orbitals of increased energy, \[{{\rm{e}}_{\rm{g}}}\] set.
This splitting of the degenerate levels due to the presence of ligands in a definite geometry is termed as crystal field splitting.

Thus, the energy of the two \[{{\rm{e}}_{\rm{g}}}\] orbitals will increase by \[
\dfrac{{{\rm{3}}}}{{\rm{5}}}{\rm{ \times (magnitude \ of \ crystal \ field \ splitting)}}\] and that of the three will decrease by \[\dfrac{{{\rm{2}}}}{{\rm{5}}}{\rm{ \times (magnitude \ of \ crystal \ field \ splitting)}}\].
The crystal field splitting relies upon the field generated by the ligand and the charge on the metal ion.

In the case of \[{{\rm{[Ti(}}{{\rm{H}}_{\rm{2}}}{\rm{O)]}}^{{\rm{3 + }}}}\] , Ti ion has only one electron.
The single d electron obtains the lower energy \[{{\rm{t}}_{{\rm{2g}}}}\] orbitals.

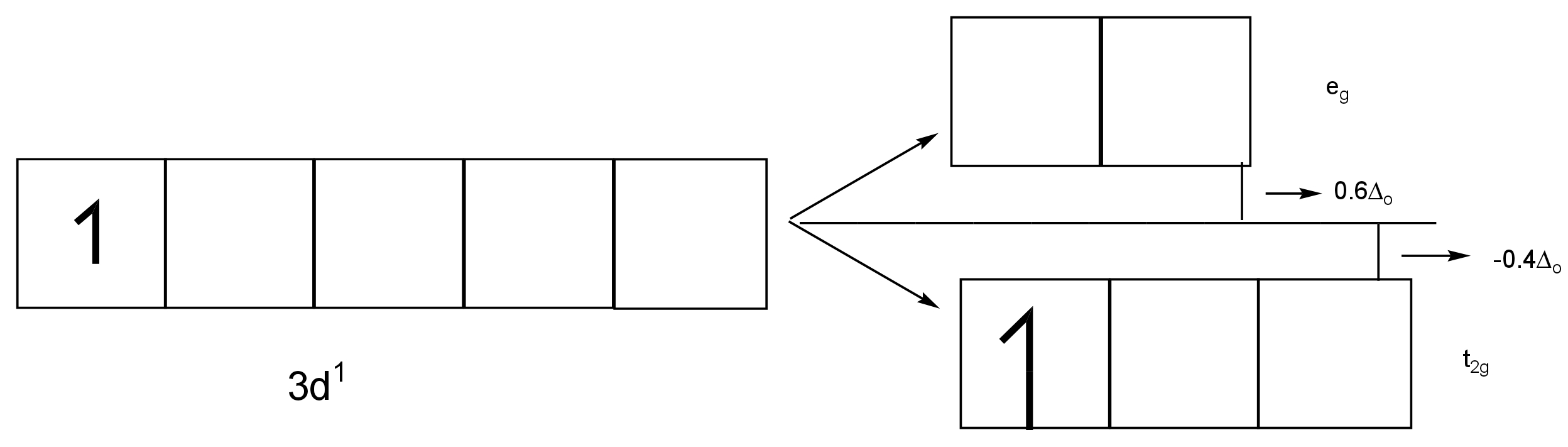
Image: Splitting of d-orbitals

Here, the magnitude of crystal field stabilisation energy is \[{\rm{20,300c}}{{\rm{m}}^{{\rm{ - 1}}}}\].
\[\begin{array}{*{20}{l}}{{\rm{IkJ/mol = 83}}{\rm{.7c}}{{\rm{m}}^{ - 1}}}\\{{\rm{1c}}{{\rm{m}}^{ - 1}}{\rm{ = }}\dfrac{1}{{83}}{\rm{kJ/mol}}{\rm{.}}}\end{array}\]

The crystal field stabilisation energy, CFSE
 \[{\rm{ = ( - 0}}{\rm{.4)(20300)}}\dfrac{1}{{83.7}}{\rm{kJmo}}{{\rm{l}}^{{\rm{ - 1}}}}\]
\[{\rm{ = - 97}}{\rm{.01kJmo}}{{\rm{l}}^{{\rm{ - 1}}}}\]

So, \[{\rm{ - 97}}{\rm{.01kJmo}}{{\rm{l}}^{{\rm{ - 1}}}}\] energy is the crystal field stabilisation energy.

Note: For central metal ions having two and three d electrons, they will occupy the \[{{\rm{t}}_{{\rm{2g}}}}\] orbitals individually by Hund’s rule.

For ions having 4 electrons in the d-orbital, two possible ways of electrons are there
(i) the fourth electron could either join the \[{{\rm{t}}_{{\rm{2g}}}}\] level and couple with an existing electron, or
(ii) it will avoid pairing and join \[{{\rm{e}}_{\rm{g}}}\] level.

It depends on the magnitude of the crystal field splitting and the pairing energy, P

(i) If the magnitude of crystal field splitting is less P, the fourth electron joins one of the orbitals having three electrons in \[{{\rm{t}}_{{\rm{2g}}}}\] and 2 electrons in \[{{\rm{e}}_{\rm{g}}}\].

Ligands for which the magnitude of crystal field splitting is less than P are recognized as weak field ligands and form high spin complexes.