Question

The effective resistance between the points $A$ and $B$ in the circuit shown in Fig. will be:

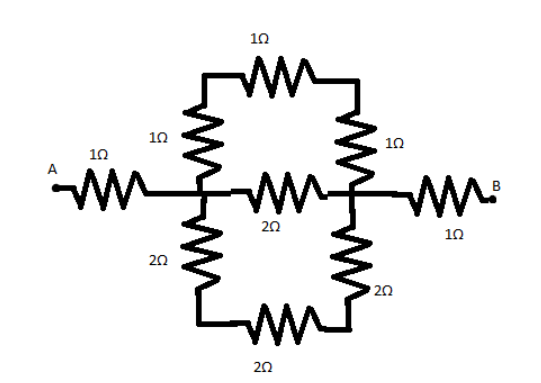
(A) $6\Omega $
(B) $3\Omega $
(C) $15\Omega $
(D) $10\Omega $

Answer 1

Hint: We will use the general formula of adding resistances here. The net resistance between points $A$ and $B$ is the same as the addition of net resistances between points $A$ and $C$, $C$ and $D$, $D$ and $B$ which is given in the below figure. We will simplify the resistances using the formulas below.
Formula used: Resistance calculation in series ${R_{series}} = {R_1} + {R_2} + ...$
Resistance calculation in parallel $\dfrac{1}{{{R_{parallel}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...$

Complete Step by step solution:

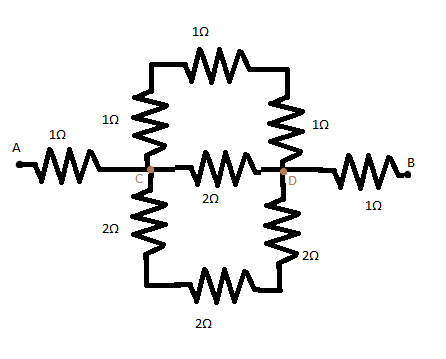
In the given diagram,
Net resistance between $A$ and $B$ is calculated by adding the net resistances between $A$ and $C$, $C$ and $D$, $D$ and $B$ since they will be in series.
Therefore, ${R_{AC}} = 1\Omega $ as can be seen, from the figure.
In the calculation of ${R_{CD}}$, we see that the three $1\Omega $ resistances are in series. We use the series resistance formula here to get the net resistance as $1\Omega + 1\Omega + 1\Omega = 3\Omega $ on the top branch.
Similarly, the three $2\Omega $ resistances are also in series. We use the series resistance formula again to get the net resistance as $2\Omega + 2\Omega + 2\Omega = 6\Omega $ on the bottom branch.
These $3\Omega $ net resistance of the top branch, $2\Omega $ resistance of the middle branch, and $6\Omega $ net resistance of the bottom branch are now in parallel.
Hence, we use the formula for resistances in parallel to get the net resistance as $\dfrac{1}{{{R_{parallel}}}} = \dfrac{1}{{3\Omega }} + \dfrac{1}{{2\Omega }} + \dfrac{1}{{6\Omega }}$
$ \Rightarrow \dfrac{1}{{{R_{parallel}}}} = \dfrac{{2 + 3 + 1}}{{6\Omega }} = \dfrac{1}{{1\Omega }}$
$\therefore {R_{parallel}} = 1\Omega $
This is the net resistance between points $C$ and $D$. Thus ${R_{CD}} = 1\Omega $.
The resistance between points $D$ and $B$, i.e. ${R_{DB}} = 1\Omega $ as can be seen from the figure given.
Now the resistances ${R_{AC}}$, ${R_{CD}}$ and ${R_{DB}}$ are in series.
We will therefore use the series formula for summation of resistances.
${R_{net}} = {R_{AC}} + {R_{CD}} + {R_{DB}} = 1\Omega + 1\Omega + 1\Omega = 3\Omega $
$ \Rightarrow {R_{net}} = 3\Omega $
Thus the net resistance between the points $A$ and $B$ is equal to $3\Omega $.

Therefore option (B) is the correct answer.

Note: The other process of calculating the equivalent or net resistance between two points includes assuming a current of $1A$ flowing through the circuit and calculating the net voltage drops from a specific point. After finding the net voltage drop, we will use the formula $V = IR$, to find the $R$, i.e. effective resistance in case of complicated circuits.