Question

The earth's magnetic field at the equator is approximately 0.4G. Estimate the earth's dipole moment.
A) $1.05 \times {10^{23}}A{m^2}$
B) $1.05 \times {10^{ - 23}}A{m^2}$
C) $5.01 \times {10^{23}}A{m^2}$
D) $5.01 \times {10^{ - 23}}A{m^2}$

Answer 1

Hint: To solve this question, we have to imagine that a bar magnet is kept at the equator of the earth. After that, we just have to find the relation between the dipole moment of that bar magnet and the magnetic field of that bar magnet. We can easily substitute the values to find the dipole moment of that magnet which will be the required dipole moment of the earth.

Formulae used:
${B_{equatorial}} = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{M}{{{d^3}}}$
Here ${\mu _0}$ is the permeability of free space, $M$ is the dipole moment of the magnet, $d$ is the distance of the point from the equator of the magnet, and ${B_{equatorial}}$ is the magnetic field of the magnetic field at the equator of the magnet.

Complete step by step solution:
Let us consider that a bar magnet is placed along the equator of the earth.

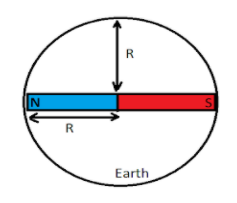
We know that,
$ \Rightarrow {B_{equatorial}} = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{M}{{{d^3}}}$

Here ${\mu _0}$ is the permeability of free space, $M$ is the dipole moment of the magnet, $d$ is the distance of the point from the equator of the magnet, and ${B_{equatorial}}$ is the magnetic field of the magnetic field at the equator of the magnet.
Let this be equation 1.
From the above diagram, we can say that
$ \Rightarrow d = R = 6400Km = 6400 \times {10^3}m$
Also, the value of the magnetic field is given as
$ \Rightarrow B = 0.4G = 0.4 \times {10^{ - 4}}T$
So equation 1 becomes,
$ \Rightarrow 0.4 \times {10^{ - 4}} = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{M}{{{{\left( {6400 \times {{10}^3}} \right)}^3}}}$
$ \Rightarrow M = \dfrac{{0.4 \times {{10}^{ - 4}} \times {{\left( {6400 \times {{10}^3}} \right)}^3}}}{{{{10}^{ - 7}}}} = 1.05 \times {10^{23}}A{m^2}$
$ \Rightarrow M = 1.05 \times {10^{23}}A{m^2}$
Earth’s dipole moment at the equator will be $1.05 \times {10^{23}}A{m^2}$.

From this, we can conclude that option (A) is the correct answer.

Note: The values of magnetic fields at the equator and the axis of the bar magnet are different. So we have to be very careful while solving questions related to the magnetic field or dipole moment of any magnet to avoid incorrect answers.