Question

The correct curve between admittance (Y) and frequency (f) in an anti-resonant circuit will be
A)

B)

C)

D)

Answer 1

Hint: Let us discuss in brief about an anti-resonant circuit. A parallel circuit containing a resistor, an inductor and a capacitor will produce an anti-resonance circuit (also called parallel resonance circuit) if the net current through the combination is in phase with the voltage. The remarkable point is that at resonance, the anti-resonant circuit produces the same equation as for the series resonance circuit.

Formula Used:
\[Y=\dfrac{1}{Z}\] , \[Z=\dfrac{V}{I}\]

Complete step by step solution:
In the hint section, we mentioned that the formula for the anti-resonant circuit is the same as that for a series resonance circuit. As such, it should make no difference if the inductor or capacitor are connected in parallel or series. But that is not the case.

In the anti-resonant circuit, the reactance (which is the resistance due to capacitor and inductor) of the circuit is maximum. If the impedance of a circuit is at its maximum, then consequently, the admittance must be at its minimum. The relation between admittance and impedance can be given as \[Y=\dfrac{1}{Z}\] where \[Y\] is the admittance and \[Z\] is the impedance. The current and the impedance can be related as \[Z=\dfrac{V}{I}\] where \[V\] denotes the voltage and \[I\] denotes the current. The admittance can hence be written as \[Y=\dfrac{I}{V}\] . Thus, if the reactance of the circuit is at maximum, it implies that the current in the circuit will be at a minimum.
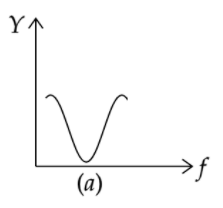
Among the options given above, option (A) is the only option that depicts admittance attaining a minimum value.

Therefore, option (A) is the correct answer.

Note: In contrast to the series resonance circuit, the resistor in an anti-resonant circuit has a damping effect on the circuit bandwidth. Also, since the current is constant for any value of impedance, the waveform of the voltage for an anti-resonant circuit will have the same shape as that of the total impedance.