Question

The average kinetic energy of a simple harmonic oscillator is \[2J\] and its total energy is\[5J\]. Its minimum potential energy is:
A. \[1J\]
B. \[1.5J\]
C.\[2J\]
D. \[3J\]

Answer 1

Hint: Before we proceed with the problem, it is necessary to know the simple harmonic oscillator. A simple harmonic oscillator is a system that is composed of a mass\[m\]. When a force \[F\] is applied to the mass, it starts to oscillate between mean positions and extreme positions.

Complete step by step solution:
In an oscillator, there are two extreme positions at \[{E_1}\]and\[{E_2}\]. The mass oscillates between these two positions. Therefore, an oscillator has,
A. Maximum K.E. and minimum P.E. at the mean position.
B. Minimum K.E. and maximum P.E. at the extreme position.

We know that total energy is equivalent to the sum of K.E. and P.E.

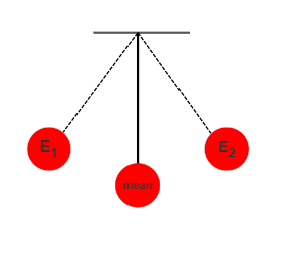
Image: Simple pendulum

Here it given that total energy \[ = 5J\]
Average kinetic energy \[\langle KE\rangle = 2J\]
We know that average kinetic energy is calculated by the formula,
\[\langle KE\rangle = \dfrac{{K{E_{\max }} + K{E_{\min }}}}{2}\]
\[\begin{array}{l}2 = \dfrac{{K{E_{\max }} + 0}}{2}\\ \Rightarrow K{E_{\max }} = 4\end{array}\]
When the potential energy is minimum then kinetic energy is maximum. Therefore total energy can be written as
\[TE = K{E_{\max }} + P{E_{\min }}\]
\[\Rightarrow 5 = 4 + P{E_{\min }}\]
\[\Rightarrow P{E_{\min }} = 5 - 4 = 1J\]
\[\therefore P{E_{\min }} = 1J\]

Hence, option \[A\] is correct.

Note: In the concept of the simple harmonic oscillator, students are often confused between the energies at the mean position and at the extreme position. At the mean position, the mass \[m\] is at rest i.e., \[x = 0\], so P.E. is zero and K.E. is maximum. At the extreme position, the mass \[m\] is at maximum distance from the mean position. So their P.E. is maximum while K.E. is zero.