Question

The angle of deviation $(\delta )$ vs angle of incidence $(i)$ is plotted for a prism. Pick up the correct statements.

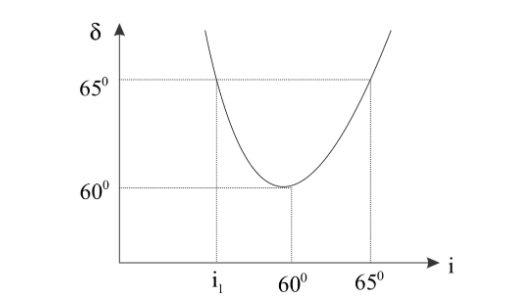
(A) The angle of the prism is ${60^0}$.
(B) The refractive index of prism is $n = \sqrt 3 $.
(C) The curve of $\delta {\text{ vs }}i$ is parabolic.
(D) For the deviation to be ${65^0}$ the angle of incidence to be ${i_1} = {55^0}$.

Answer 1

Hint We know that deviation of prism is given by $\delta = i + e - A$, where $\delta $ is deviation, $i$ is angle of incidence, $e$ is angle of emergence and $A$ is angle of prism. For minimum deviation, $i = e$. Using these equations, we find the angle of the prism. Using minimum deviation, we find a refractive index of prism. After this, find ${i_1}$ using the given information.

Complete step by step solution
We know that deviation of prism is given by $\delta = i + e - A$, where $\delta $ is deviation, $i$ is angle of incidence, $e$ is angle of emergence and $A$ is angle of prism. For minimum deviation, $i = e$.
From the figure, for minimum deviation, $\delta = {60^0}$ and also ${i_1} = {60^0}$.
For minimum deviation, $\delta = 2i - A$ or $A = 2i - \delta $.
After putting value in above equation, we get
$A = 2 \times 60 - 60 = {60^0}$.
Now refractive of given is given by
$n = \dfrac{{\sin \left( {\dfrac{{A + \delta }}{2}} \right)}}{{\sin \dfrac{A}{2}}}$
Then, $n = \dfrac{{\sin 60}}{{\sin 30}} = \sqrt 3 $.
Here for angle of deviation ${65^0}$, angle of emergence is given in figure that is $e = {70^0}$,
Then, ${\delta _1} = {i_1} + e - A$ or ${i_1} = {\delta _1} - e + A$
${i_1} = 65 - 70 + 60 = {55^0}$.
From the graph we can see that the curve of $\delta {\text{ vs }}i$ is parabolic.

Hence all options are correct.

Note We know that of each angle of deviation there are two points on the graph, these two are angle of incidence and angle of emergence and always exist in pairs. These angles are such that if we take angle of emergence as angle of incidence the angle of emergence for that case is angle of incident of given case.