
The angle of depression of the top and the bottom of a building 50m high are observed from the top of a tower are \[30^\circ \] and \[60^\circ \] respectively. Find the height of the tower and also the horizontal distance between the building and the tower.
Answer
523.1k+ views
Hint: Draw the diagram of the given problem statement for a better understanding of the situation. Use the trigonometric ratios, that are $\sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$ and $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$ in the physical triangle formed to find the height of the tower and horizontal distance between the building and the tower.
Complete step by step answer:
Since it is given that the angle observed from the top of the tower to the top and bottom of the building are \[30^\circ \] and \[60^\circ \]respectively, we can draw a diagram representing the condition.
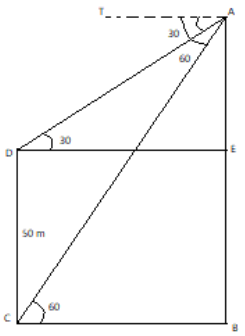
In the diagram, A represents the top of the tower, AB represents the height of the tower, DC represents the building of height 50 metres.
It is given in the question that the angle $\angle TAD$ is \[30^\circ \] and the angle $\angle TAC$ is \[60^\circ \].
By the property of the corresponding angles of the parallel lines, we can say that the angle $\angle ADE$is \[30^\circ \] and the angle $\angle ACB$ is \[60^\circ \].
In the triangle $ADE$, we can say
\[\tan {30^ \circ } = \dfrac{{{\text{AE}}}}{{DE}}\]
On further simplifying
$
\dfrac{1}{{\sqrt 3 }} = \dfrac{{{\text{AE}}}}{{DE}} \\
\sqrt 3 {\text{AE = DE}} \\
$
Similarly, in the triangle ${\text{ACB}}$
\[\tan {60^ \circ } = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}\]
On further simplifying
$
\sqrt 3 = \dfrac{{{\text{AB}}}}{{{\text{BC}}}} \\
\sqrt 3 {\text{BC = AB}} \\
$
From the figure we infer that,
${\text{BC = DE}}$
$
{\text{AB = AE + EB}} \\
{\text{EB = CD = 50}} \\
{\text{AB = AE + 50}} \\
$
Substituting the value ${\text{AE + 50}}$ for ${\text{AB}}$ and ${\text{DE}}$ for ${\text{BC}}$ in the equation \[\sqrt 3 {\text{BC = AB}}\], we get
\[\sqrt 3 {\text{DE = AE + 50}}\]
Also, \[\sqrt 3 {\text{AE = DE}}\]
Thus the expression becomes \[\sqrt 3 \left( {\sqrt 3 {\text{AE}}} \right){\text{ = AE + 50}}\]
We can solve the expression to find the value of ${\text{AE}}$
$
3{\text{AE = AE + 50}} \\
{\text{2AE = 50}} \\
{\text{AE = 25}} \\
$
Substituting the value 25 for ${\text{AE}}$ in the equation ${\text{AB = AE + 50}}$ to find the height of the tower, and in the equation \[\sqrt 3 {\text{AE = DE}}\] to find the horizontal distance between the building and the tower.
$
{\text{AB = 25 + 50}} \\
{\text{AB = 75}} \\
$
\[{\text{DE}} = \sqrt 3 \left( {25} \right)\]
Thus the height of the tower is 75 m, and the horizontal distance between the building and the tower is $25\sqrt 3 $m.
Note: In a right angled triangle, the $\tan \theta $ is the equal to $\dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$, where perpendicular is the side opposite to the angle $\theta $, and $\sin \theta $ is the equal to $\dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$, where perpendicular is the side opposite to the angle $\theta $.
Complete step by step answer:
Since it is given that the angle observed from the top of the tower to the top and bottom of the building are \[30^\circ \] and \[60^\circ \]respectively, we can draw a diagram representing the condition.

In the diagram, A represents the top of the tower, AB represents the height of the tower, DC represents the building of height 50 metres.
It is given in the question that the angle $\angle TAD$ is \[30^\circ \] and the angle $\angle TAC$ is \[60^\circ \].
By the property of the corresponding angles of the parallel lines, we can say that the angle $\angle ADE$is \[30^\circ \] and the angle $\angle ACB$ is \[60^\circ \].
In the triangle $ADE$, we can say
\[\tan {30^ \circ } = \dfrac{{{\text{AE}}}}{{DE}}\]
On further simplifying
$
\dfrac{1}{{\sqrt 3 }} = \dfrac{{{\text{AE}}}}{{DE}} \\
\sqrt 3 {\text{AE = DE}} \\
$
Similarly, in the triangle ${\text{ACB}}$
\[\tan {60^ \circ } = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}\]
On further simplifying
$
\sqrt 3 = \dfrac{{{\text{AB}}}}{{{\text{BC}}}} \\
\sqrt 3 {\text{BC = AB}} \\
$
From the figure we infer that,
${\text{BC = DE}}$
$
{\text{AB = AE + EB}} \\
{\text{EB = CD = 50}} \\
{\text{AB = AE + 50}} \\
$
Substituting the value ${\text{AE + 50}}$ for ${\text{AB}}$ and ${\text{DE}}$ for ${\text{BC}}$ in the equation \[\sqrt 3 {\text{BC = AB}}\], we get
\[\sqrt 3 {\text{DE = AE + 50}}\]
Also, \[\sqrt 3 {\text{AE = DE}}\]
Thus the expression becomes \[\sqrt 3 \left( {\sqrt 3 {\text{AE}}} \right){\text{ = AE + 50}}\]
We can solve the expression to find the value of ${\text{AE}}$
$
3{\text{AE = AE + 50}} \\
{\text{2AE = 50}} \\
{\text{AE = 25}} \\
$
Substituting the value 25 for ${\text{AE}}$ in the equation ${\text{AB = AE + 50}}$ to find the height of the tower, and in the equation \[\sqrt 3 {\text{AE = DE}}\] to find the horizontal distance between the building and the tower.
$
{\text{AB = 25 + 50}} \\
{\text{AB = 75}} \\
$
\[{\text{DE}} = \sqrt 3 \left( {25} \right)\]
Thus the height of the tower is 75 m, and the horizontal distance between the building and the tower is $25\sqrt 3 $m.
Note: In a right angled triangle, the $\tan \theta $ is the equal to $\dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$, where perpendicular is the side opposite to the angle $\theta $, and $\sin \theta $ is the equal to $\dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$, where perpendicular is the side opposite to the angle $\theta $.
Recently Updated Pages
Find the value of sin 50 circ sin 70 circ + sin 10 class 10 maths JEE_Main

The angle of depression of the top and the bottom of class 10 maths JEE_Main

The amount of work in a leather factory is increased class 10 maths JEE_Main

The side BC of a triangle ABC is bisected at D O is class 10 maths JEE_Main

The circumference of the base of a 24 m high conical class 10 maths JEE_Main

JEE Main 2026 Session 1 Exam Dates Revised | New Exam Schedule Released

Trending doubts
JEE Main 2026: City Intimation Slip and Exam Dates Released, Application Form Closed, Syllabus & Eligibility

JEE Main 2026 City Intimation Slip Live (OUT): Paper 1 & Paper 2 Exam Dates Announced

JEE Main Syllabus 2026: Download Detailed Subject-wise PDF

JEE Main Marks vs Percentile 2026: Calculate Percentile and Rank Using Marks

JEE Mains Admit Card 2026 Live Updates: Download Hall Ticket at jeemain.nta.nic.in

JEE Main 2026 Exam Centres (OUT) – Latest Examination Centre and Cities List

Other Pages
Pregnancy Week and Due Date Calculator: Find How Far Along You Are

NCERT Solutions For Class 10 Maths Chapter 11 Areas Related to Circles (2025-26)

NCERT Solutions For Class 10 Maths Chapter 12 Surface Areas and Volumes (2025-26)

All Mensuration Formulas with Examples and Quick Revision

Complete List of Class 10 Maths Formulas (Chapterwise)

NCERT Solutions for Class 10 Maths Chapter 13 Statistics




