Question

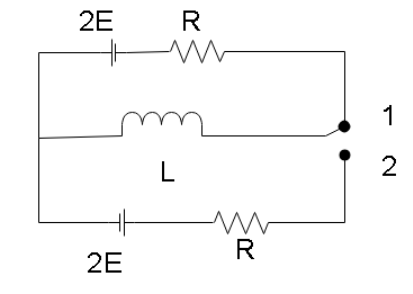
Switch was in position 1 for a long time. It is suddenly switched to position 2. Find voltage drop across the inductor immediately after the switch is toggled.

Answer 1

Hint: In this solution, we will first calculate the potential difference developed across the inductor when the switch is in position 1 for a long time. Then, when the switch is toggled, at that instant, the inductor wouldn’t allow a change in potential across the inductor.
Formula used: In this solution, we will use the following formula
- Ohm’s law: \[V = IR\] where $V$ is the potential difference across a resistor, $I$ is the current, and $R$ is its resistance

Complete step by step answer:
When the circuit has been in state 1 for a long time, the circuit will have achieved a steady-state. In this state, the inductor will act as a straight wire and hence the current in the circuit can be determined from ohm’s law as:
$I = \dfrac{E}{R}$
This amount of current will also be flowing through the inductor however in steady-state, there won’t be any potential difference across it. Now, when the switch is toggled to position 2, suddenly there will be a change in the potential of the circuit which will try to change the current in the circuit. The inductor will induce a potential difference across itself to avoid the flux from changing across it. The potential induced will have a direction such that it will oppose the battery and will have a magnitude corresponding to the current that was flowing through it as
${E_{ind}} = IR = E$
Then in position two, the net EMF in the circuit will be
$V = 2E - {E_{ind}} = E$
Since the resistance in state 2 is also $R$., the current in the circuit will be
$I = \dfrac{E}{R}$.
Hence the current in the circuit will be $I = \dfrac{E}{R}$ at the instant when the switch is toggled.

Note: When deciding the EMF that will be induced in the inductor, we must take care of whether it will oppose or support the battery. For an inductor, it will always induce an EMF to oppose an external battery to avoid the change of magnetic flux inside it and hence the induced voltage will always oppose the external battery. However, in steady-state, the potential drop across the inductor would drop to 0.