Question

Suppose the drift velocity ${v_d}$ in a material varied with the applied electric field $E$ as: ${v_d} \propto \sqrt E $. Then V – I graph for a wire made of such a material is best given by
(A)

(B)

(C)

(D)

Answer 1

Hint: To solve this question, we need to use the formula for the drift velocity in terms of the current. Then using the given relation we can get the relation between the current and the voltage with the help of which we can predict the shape of the plot.

Formula used: The formula used to solve this question is
$I = neA{v_d}$, here $I$ is the current in a conductor having area of cross section $A$, $n$ is the number density of the electrons of charge $e$ and drift velocity of ${v_d}$.

Complete step-by-step solution:
The relation between the drift velocity and the applied electric field is given in the question as
${v_d} \propto \sqrt E $
We know that we can replace the proportionality sign in a relation with the equal sign by introducing a constant in the right hand side of the relation. So we can write the above relation as as
${v_d} = k\sqrt E $
On squaring both sides of the above equation, we get
${v_d}^2 = {k^2}E$
$ \Rightarrow E = \dfrac{{{v_d}^2}}{{{k^2}}}$................(1)
Now, we know that the potential difference across a conductor is related to the uniform electric field present in the conductor by the relation
$V = \dfrac{E}{l}$ (here $l$ is the assumed length of the material given in the question)
Substituting (1) in the above equation, we get
$V = \dfrac{{{v_d}^2}}{{{k^2}l}}$ ……………….(2)
Now, we know that the current in a conductor is related to the drift velocity of the electrons of the conductor as
$I = neA{v_d}$...................(3)
$ \Rightarrow {v_d} = \dfrac{I}{{neA}}$........................(4)
Putting (4) in (2) we get
$V = \dfrac{{{{\left( {\dfrac{I}{{neA}}} \right)}^2}}}{{{k^2}l}}$
$V = \dfrac{{{I^2}}}{{{n^2}{e^2}{A^2}{k^2}l}}$
Now, we know that the number density, charge of electron, area of cross section of the material, and the length of the conductor are all constants. So we can write the above equation as
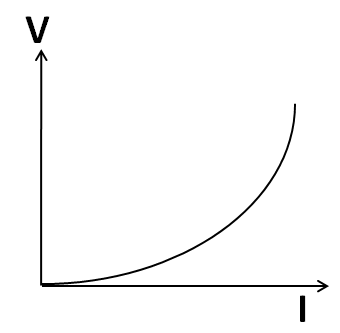
$V = c{I^2}$
Comparing the equation $y = k{x^2}$, we get the V-I relation as a parabolic equation. So its plot should a parabola as shown below

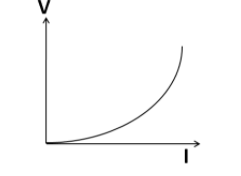
Hence, the correct answer is option A.

Note: From the Ohm’s law we know that the relation between the current and the voltage is linear across a conductor. So we should have got a linear plot according to the Ohm’s law. But the Ohm’s law is only valid if the resistance of the conductor is constant. In this case the resistance of the material used is not constant, and therefore we didn’t get a linear V-I plot.