Question

Starting from rest a car moves with uniform acceleration and attains a velocity of $90{\text{km/h}}$ in \[25\;{\text{s}}\]. It then moves with uniform speed for $30\;{\text{s}}$ and is then brought to rest in \[20\;{\text{s}}\] under uniform retardation. Find total distance travelled using velocity - time graph.

Answer 1

Hint: In this question, the concept of the velocity time graph will be used, that is the area under the curve of the graph represents the total distance travelled. Plot the velocity-time graph according to the question given. Find the area of the graph which will give the result for total distance travelled using velocity - time graph.

Complete step by step answer:
Firstly, to solve this question, we have to convert the velocity given for the car in ${\text{m/s}}$format.
So,
$ \Rightarrow 90{\text{km/h}} = 90 \times \dfrac{{1000}}{{360}}{\text{m/s}} = 25{\text{m/s}}$
Now, we plot the velocity-time graph (or the v-t graph) for the question, as shown below: -

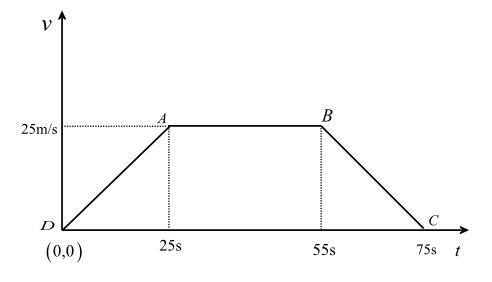
The above diagram represents the velocity time graph (v-t graph) for the question.
As we have given in the question, velocity of the car is plotted in the $y$-axis and time is plotted in the $x$ -axis.
In case of $x$ -axis (that is for plotting time): The car moves with uniform acceleration and attains a velocity of $25{\text{m/s}}$ in\[25{\text{ }}s\], so the first point is given as \[25{\text{ }}s\]. It then moves with uniform speed for$30s$, so the next point is given as $55\;{\text{s}}$ $(25 + 30 = 55s)$. Then the car is brought to rest in $20\;{\text{s}}$, so the last point is given as $75\;{\text{s}}$ $\left( {25 + 30 + 20 = 75\;{\text{s}}} \right)$.
Now, according to the formula for displacement, we have to calculate the Area under the velocity-time graph. (As Displacement= Area under velocity-time graph)
So we can clearly see in the figure that the figure forming in the velocity-time graph is a Trapezoid.
So,
\[ \Rightarrow {\text{Area of Trapezoid}} = \dfrac{1}{2} \times \left( {{\text{Sum of Parallel Sides}}} \right) \times \left( {{\text{Distance between them}}} \right)\]
Here, Parallel sides (according to the v-t graph) are \[AB\]and \[CD\]. And the distance between them is $25{\text{m/s}}$.
\[ \Rightarrow {\text{Area of Trapezoid}} = \dfrac{1}{2} \times \left( {AB + CD} \right) \times 25\]
Now, we substitute the given values as,
\[ \Rightarrow {\text{Area of Trapezoid}} = \dfrac{1}{2} \times (30 + 75) \times 25\]
After simplification we get,
\[ \Rightarrow {\text{Area of Trapezoid}} = 1312.5\;{\text{m}}\]
Hence, the total distance travelled using velocity-time graph is $1312.5\;{\text{m}}$.

Note: Mistakes occur while plotting the velocity-time graph. In $x$-axis, time plotted should be taken cautiously as the timestamps are summed up continuously and plotted. Conversion of units is done for the ease of calculation.