Question

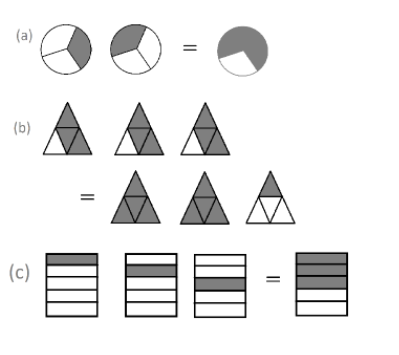
Some fractional equations have been given with some pictures. Match the equations with the proper pictures.
(i) $3\times \dfrac{1}{5}=\dfrac{3}{5}$
(ii) $2\times \dfrac{1}{3}=\dfrac{2}{3}$
(iii) $3\times \dfrac{3}{4}=2\dfrac{1}{4}$

Answer 1

Hint: We have been provided with a fractional equation. It consists of multiplication of an integer with a fraction. We need to match the equations in such a way that the picture consists of the fraction as a shaded part of the geometrical figure of that picture. Also, the number of such shaded figures has to be exactly equal to the integer.

Complete step-by-step answer:
We will go through all the pictures one by one.
So, for the first picture with a geometrical figure of a circle we get that there are two such circles.
Each circle has been divided into $3$parts.
The shaded area is in total $1$ parts of that $3$parts circle.
The picture consists of the fraction as a shaded part of the geometrical figure of that picture.
So, the shaded part in that figure can be expressed as the fraction.
The shaded parts are $1$ out of $3$ parts.
So, it can be expressed as $\dfrac{1}{3}$.
Now, number of such similar figures of circle is $2$.
So, we can count this $2$as the integer multiplied with the fraction as the number of such shaded figures has to be exactly equal to the integer.
Now the end result of those two circles is the rightmost circle, where we have got the circle’s been divided into $3$ parts. The only difference being here we have taken $2$ consecutive parts of that $3$ parted circle.
So, we can express it as $\dfrac{2}{3}$.
It will be equal to the solution of the multiplication of the integer with the fraction.
So, we express it as $2\times \dfrac{1}{3}=\dfrac{2}{3}$.
Now, for the second picture with geometrical figure of triangle we get that there are three such triangles.
Each triangle has been divided into $4$ parts.
The shaded area is in total $3$ parts of that $4$ parts triangle.
The picture consists of the fraction as a shaded part of the geometrical figure of that picture.
So, the shaded part in that figure can be expressed as the fraction.
The shaded parts are $3$ out of $4$ parts.
So, it can be expressed as $\dfrac{3}{4}$.
Now, the number of such similar figures of triangles is $3$.
So, we can count this $3$as the integer multiplied with the fraction as the number of such shaded figures has to be exactly equal to the integer.
Now the end result of those three triangles is the triangles on the right side of the ‘=’, where we have got two full triangles and the third triangle’s been divided into $4$ parts. The only difference being here we have taken $1$ part of that $4$ parted triangle.
So, we can express it as $2\times 1+\dfrac{1}{4}$.
It is equal to $2\dfrac{1}{4}$.
It will be equal to the solution of the multiplication of the integer with the fraction.
So, we express it as $3\times \dfrac{3}{4}=2\dfrac{1}{4}$.


And, for the third picture with a geometrical figure of rectangle we get that there are three such rectangles.
Each rectangle has been divided into $5$ parts.
The shaded area is in total $1$ part of that $5$ parts rectangle.
The picture consists of the fraction as a shaded part of the geometrical figure of that picture.
So, the shaded part in that figure can be expressed as the fraction.
The shaded parts are $1$ out of $5$ parts.
So, it can be expressed as $\dfrac{1}{5}$.
Now, the number of such similar figures of rectangle is $3$.
So, we can count this $3$ as the integer multiplied with the fraction as the number of such shaded figures has to be exactly equal to the integer.
Now the end result of those three rectangles is the rightmost rectangle, where we have got the rectangle’s been divided into $5$ parts. The only difference being here we have taken $3$ part of that $5$ parted rectangle.
So, we can express it as $\dfrac{3}{5}$.
It will be equal to the solution of the multiplication of the integer with the fraction.
So, we express it as $3\times \dfrac{1}{5}=\dfrac{3}{5}$.
So, the matchings are (i)-(c), (ii)-(a), (iii)-(b)
Note: We need to be careful about the third equation where a mixed fraction has been given. We don’t need to express the given integer as the fraction form. The triangles have been taken in full. Then we will consider them as integers only.
Also, in this case visualisation of shifting of the shaded parts will help to understand the problem. We can use cut out of papers to join the shaded parts to get the end result.