Question

Semi-circular ring of radius 0.5m is uniformly charged with a charge of $1.4 \times {10^{ - 9}}C$. The electric field intensity at centre of this ring is:
(A) $zero$
(B) $320V/M$
(C) $64V/M$
(D) $32V/M$

Answer 1

Hint: Here, it is important to note that the charge is distributed over an object. Hence we cannot directly apply Coulomb’s law which is valid for a point charge. Hence we need to get the electric field due to any general element and then integrate over the ring to get a net electric field at the centre.


Formula used:
$dE = \dfrac{{Kdq}}{{{r^2}}}$

Complete step-by-step solution:

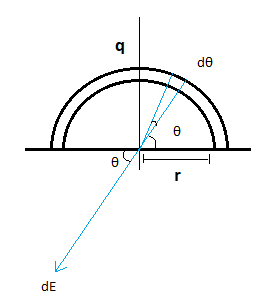
Let us consider an elementary part of the ring at an angle $\theta $ having the angular length of $d\theta $. The small charge inside the elementary part will be calculated as follows:
Total circumference
\[ \Rightarrow \pi r\]
Total charge distributed
$ \Rightarrow q$
Hence the linear charge density
$ \Rightarrow \dfrac{q}{{\pi r}}$
Thus the total charge in the element of length $rd\theta $ , will be:
$dq = \dfrac{q}{{\pi r}}rd\theta = \dfrac{{qd\theta }}{\pi }$
Now, using $dE = \dfrac{{Kdq}}{{{r^2}}}$
The electric field along –y-axis is sin component of dE,
$d{E_y} = dE\cos \theta = \dfrac{{Kq}}{{\pi {r^2}}} \times \sin \theta d\theta $
Then,${E_{net}} = \int {dE = \int {\dfrac{{Kq}}{{\pi {r^2}}} \times \sin \theta d\theta } } $
[Where ${E_{net}}$=net field in-y direction]
Or${E_{net}} = \dfrac{{Kq}}{{\pi {r^2}}} \times \int\limits_0^\pi {\sin \theta d\theta } $ [as K, q and r are constants]
As the material is present for $\theta = 0$ to$\theta = \pi $, hence are the limits.
And,${E_{net}} = \dfrac{{Kq}}{{\pi {r^2}}} \times \left( {1 - \left( { - 1} \right)} \right) = \dfrac{{2Kq}}{{\pi {r^2}}}$
On putting the values$q = 1.4 \times {10^{ - 9}}C$, $r = 0.5m$ we get;
${E_{net}} = \dfrac{{2 \times 9 \times {{10}^9} \times 1.4 \times {{10}^{ - 9}}}}{{3.14 \times {{0.5}^2}}} = 32V{m^{ - 1}}$

So, the correct answer is option (D) $32V/M$ .

Note: Students here should note that we can write ${E_y} = {E_{net}}$ as due to symmetry, the only y component of the field will contribute to the total field and the x component will come out to be zero.
This can also be easily proven by taking $d{E_x} = d{E_{net}} = \dfrac{{Kq}}{{{r^2}}} \times \cos \theta $. Also students should understand how to take the limits. If the material were present only in the first quadrant, we might have taken the limits from 0 to $\dfrac{\pi }{2}$ instead of $\pi $ .